Java 矩阵乘法详解：从原理到代码实现

在数学和计算机科学中，矩阵乘法是一项基础且重要的运算，广泛应用于图形处理、机器学习、物理模拟等领域。本文将通过一道典型的Java编程题，详细解析矩阵乘法的实现原理与代码细节。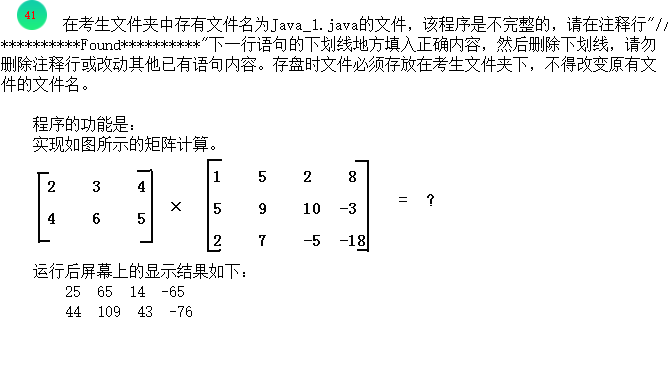

一、原题呈现

以下是关于二维数组矩阵乘法的Java程序，包含3处需要填写的空白（标记为//*********Found********），请补全代码实现矩阵乘法功能：

public class Java_1 {

    public static void main(String args[]) {
        int a[][] = {{2, 3, 4}, {4, 6, 5}};
        int b[][] = {{1, 5, 2, 8}, {5, 9, 10, -3}, {2, 7, -5, -18}};
        int c[][] = new int[2][4];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 4; j++) {
                //*********Found********
                c[i][j] = ___________;
                //*********Found********
                for (int k = ___________; k < ___________; k++) 
                    //*********Found********
                    c[i][j] ___________ a[i][k]*b[k][j];
                System.out.print(c[i][j] + "  ");
            }
            System.out.println();
        }
    }
}

二、空白解析与解答

要解决这道题，我们需要先理解矩阵乘法的数学原理，再结合代码逻辑补全空白。

1. 第一处空白：初始化累加变量

答案：0

//*********Found********
c[i][j] = 0;

解析：
矩阵乘法中，结果矩阵c的每个元素c[i][j]是通过累加运算得到的（即多个乘积的和）。为确保累加结果正确，必须先将c[i][j]初始化为0。虽然Java中int数组的默认值是0，但显式初始化是良好的编程习惯，能避免后续代码修改时可能出现的逻辑错误。

2. 第二处空白：控制内层循环范围

答案：0，3

//*********Found********
for (int k = 0; k < 3; k++)

解析：
内层循环变量k的作用是遍历矩阵a的列和矩阵b的行，实现对应元素的相乘累加。根据题目中矩阵的维度：

矩阵a是2行3列（列索引范围为0~2）
矩阵b是3行4列（行索引范围为0~2）

因此，k需要从0开始，到2结束（即k < 3），才能覆盖所有需要参与运算的元素。

3. 第三处空白：实现累加运算

答案：+=

//*********Found********
c[i][j] += a[i][k] * b[k][j];

解析：
矩阵乘法的核心公式是：
c[i][j] = a[i][0]×b[0][j] + a[i][1]×b[1][j] + a[i][2]×b[2][j]

+=运算符用于将每次计算的a[i][k]×b[k][j]累加到c[i][j]中，等价于：
c[i][j] = c[i][j] + a[i][k]×b[k][j]

通过循环遍历k的取值（0~2），即可完成累加计算。

三、完整代码实现

四、程序运行与结果分析

运行流程

矩阵定义：
- 矩阵a：2行3列，元素为{{2, 3, 4}, {4, 6, 5}}
- 矩阵b：3行4列，元素为{{1, 5, 2, 8}, {5, 9, 10, -3}, {2, 7, -5, -18}}
- 结果矩阵c：2行4列（根据矩阵乘法规则，2×3矩阵与3×4矩阵相乘，结果为2×4矩阵）

计算过程（以c[0][0]为例）：

c[0][0] = 0;  // 初始化
c[0][0] += a[0][0] * b[0][0] → 0 + 2×1 = 2;
c[0][0] += a[0][1] * b[1][0] → 2 + 3×5 = 17;
c[0][0] += a[0][2] * b[2][0] → 17 + 4×2 = 25;

输出结果：
程序运行后，控制台将打印结果矩阵c的所有元素：
```
25  56  22  -65  
44  107  57  -85  
```

五、核心知识点总结

矩阵乘法的数学规则
- 维度匹配：左矩阵的列数必须等于右矩阵的行数（如本题中3列 = 3行）。
- 结果维度：结果矩阵的行数 = 左矩阵行数，列数 = 右矩阵列数（如本题中2行4列）。
- 元素计算：结果矩阵c[i][j] = 左矩阵第i行与右矩阵第j列对应元素乘积的和。
三重循环的逻辑
- 外层循环（i）：控制结果矩阵c的行索引（0~1）。
- 中层循环（j）：控制结果矩阵c的列索引（0~3）。
- 内层循环（k）：遍历左矩阵的列和右矩阵的行，实现乘积累加（0~2）。
累加运算的实现
- 先初始化累加变量（c[i][j] = 0）。
- 用+=运算符逐步累加乘积结果（c[i][j] += a[i][k] * b[k][j]）。

六、常见错误与优化建议

常见错误
- 忘记初始化c[i][j]：虽然int数组默认值为0，但显式初始化能提高代码可读性和健壮性。
- 循环范围错误：如k < 4会导致数组索引越界（矩阵a和b的最大索引为2）。
- 误用赋值运算符：用=代替+=会导致累加失败，仅保留最后一次乘积结果。
优化建议
- 动态获取维度：用a[0].length（矩阵a的列数）代替硬编码的3，使代码适配任意维度的矩阵（需保证维度匹配）。
- 异常处理：添加维度校验逻辑，避免因矩阵维度不匹配导致的运行时错误。

通过本题，我们不仅掌握了矩阵乘法的代码实现，更理解了其背后的数学原理和循环逻辑。矩阵乘法是处理多维数据的基础，掌握这一知识点对后续学习更复杂的算法和数据结构具有重要意义。