找到
14
篇与
计算机二级
相关的结果
-
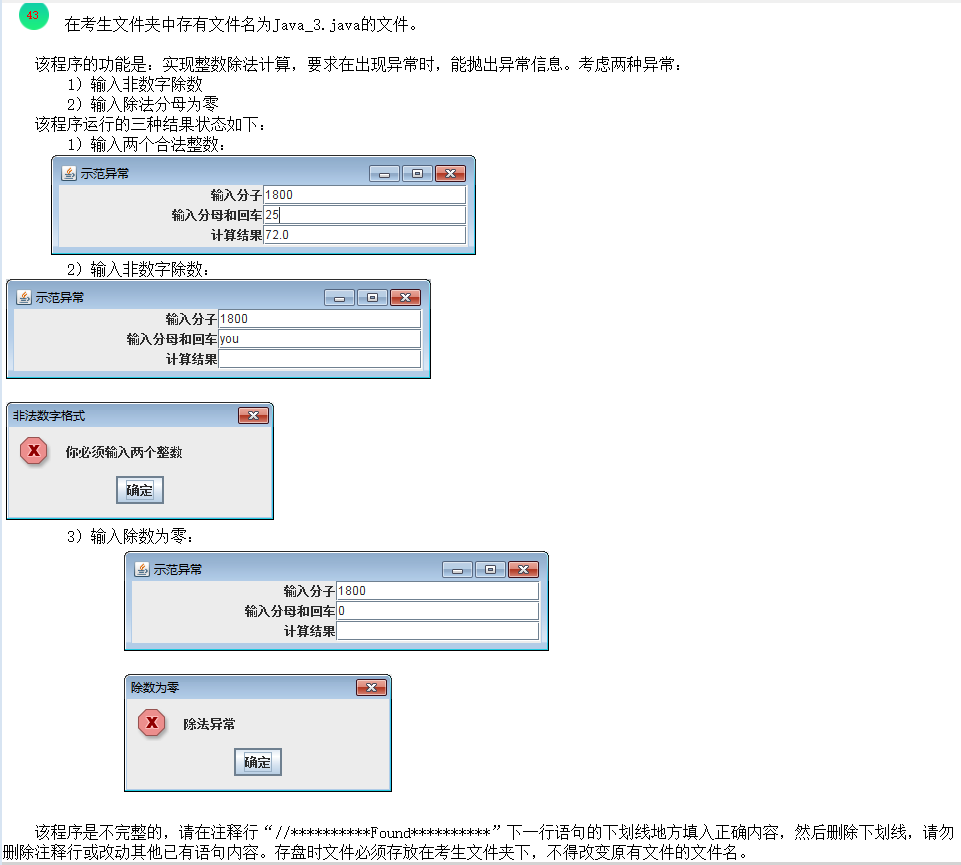
Java二级考试异常处理综合题解析：整数除法计算器实现 Java二级考试异常处理综合题解析：整数除法计算器实现 在计算机等级考试二级Java的简单应用题中，异常处理和GUI编程是重要考点。本文将通过一道综合性的整数除法计算器题目，详细解析异常处理机制、Swing组件使用以及程序调试技巧，帮助考生全面掌握这类题型的解答方法。 一、题目分析 7.png图片 题目要求 程序功能： 实现整数除法计算GUI程序 处理两种异常： 输入非数字（NumberFormatException） 除数为零（ArithmeticException） 在指定位置补全代码，不能修改已有代码 按要求显示三种运行状态的结果 程序结构分析 程序主要包含： GUI界面构建（JFrame、JTextField、JLabel） 事件处理（ActionListener） 异常处理机制（try-catch） 业务逻辑（除法运算） 二、解题思路与填空详解 原题目代码 import java.text.DecimalFormat; import javax.swing.*; import java.awt.*; import java.awt.event.*; //*********Found******** public class Java_3 extends ________ implements ActionListener { private JTextField input1, input2, output; private int number1, number2; private double result; // 初始化 public Java_3() { //*********Found******** ______( "示范异常" ); Container c = getContentPane(); c.setLayout( new GridLayout( 3, 2 ) ); c.add( new JLabel( "输入分子", SwingConstants.RIGHT ) ); input1 = new JTextField( 10 ); c.add( input1 ); c.add( new JLabel( "输入分母和回车", SwingConstants.RIGHT ) ); input2 = new JTextField( 10 ); c.add( input2 ); input2.addActionListener( this ); c.add( new JLabel( "计算结果", SwingConstants.RIGHT ) ); output = new JTextField(); c.add( output ); setSize( 425, 100 ); show(); } //处理 GUI 事件 public void actionPerformed( ActionEvent e ) { DecimalFormat precision3 = new DecimalFormat( "0.000" ); output.setText( "" ); // 空的JTextField输出 //*********Found******** ___________ { number1 = Integer.parseInt( input1.getText() ); number2 = Integer.parseInt( input2.getText() ); result = quotient( number1, number2 ); //*********Found******** output.setText(_______________________________); } catch ( NumberFormatException nfe ) { JOptionPane.showMessageDialog( this, "你必须输入两个整数", "非法数字格式", JOptionPane.ERROR_MESSAGE ); } catch ( Exception dbze ) { //*********Found******** _______________________________( this, "除法异常", "除数为零", JOptionPane.ERROR_MESSAGE ); } } // 定义求商的方法，如遇除数为零时，能抛出异常。 public double quotient( int numerator, int denominator ) throws Exception { if ( denominator == 0 ) throw new Exception(); return ( double ) numerator / denominator; } public static void main( String args[] ) { Java_3 app = new Java_3(); app.addWindowListener( new WindowAdapter() { public void windowClosing( WindowEvent e ) { e.getWindow().dispose(); System.exit( 0 ); } } ); } } /* JOptionPane类的常用静态方法如下： showInputDialog() showConfirmDialog() showMessageDialog() showOptionDialog() */第一个填空位置 public class Java_3 extends ________ implements ActionListener {需要填入：程序的主框架类 正确答案：JFrame 解释： 从后续代码可见使用了getContentPane()、setSize()、show()等方法 这些都是JFrame的特性 需要继承JFrame来创建窗口程序 第二个填空位置 ______( "示范异常" );需要填入：设置窗口标题的方法 正确答案：super 解释： 这里需要调用父类(JFrame)的构造方法设置窗口标题 或者也可以填写setTitle 但从上下文看，更可能是构造时初始化标题 第三个填空位置 ___________ { 需要填入：异常处理块开始 正确答案：try 解释： 后续有对应的catch块 需要进行异常捕获的代码必须放在try块中 这里包含可能抛出异常的整数转换和除法运算 第四个填空位置 output.setText(_______________________________);需要填入：格式化后的计算结果输出 正确答案：precision3.format(result) 解释： 前面已定义DecimalFormat precision3 = new DecimalFormat( "0.000" ) 需要将double类型的result格式化为保留3位小数 使用DecimalFormat的format方法 第五个填空位置 _______________________________( this, 需要填入：显示错误对话框的方法 正确答案：JOptionPane.showMessageDialog 解释： 查看程序末尾的注释，列出了JOptionPane的常用方法 需要显示错误消息，使用showMessageDialog 参数顺序为(父组件, 消息内容, 标题, 消息类型) 三、完整正确代码 import java.text.DecimalFormat; import javax.swing.*; import java.awt.*; import java.awt.event.*; public class Java_3 extends JFrame implements ActionListener { private JTextField input1, input2, output; private int number1, number2; private double result; public Java_3() { super( "示范异常" ); Container c = getContentPane(); c.setLayout( new GridLayout( 3, 2 ) ); c.add( new JLabel( "输入分子", SwingConstants.RIGHT ) ); input1 = new JTextField( 10 ); c.add( input1 ); c.add( new JLabel( "输入分母和回车", SwingConstants.RIGHT ) ); input2 = new JTextField( 10 ); c.add( input2 ); input2.addActionListener( this ); c.add( new JLabel( "计算结果", SwingConstants.RIGHT ) ); output = new JTextField(); c.add( output ); setSize( 425, 100 ); show(); } public void actionPerformed( ActionEvent e ) { DecimalFormat precision3 = new DecimalFormat( "0.000" ); output.setText( "" ); try { number1 = Integer.parseInt( input1.getText() ); number2 = Integer.parseInt( input2.getText() ); result = quotient( number1, number2 ); output.setText(precision3.format(result)); } catch ( NumberFormatException nfe ) { JOptionPane.showMessageDialog( this, "你必须输入两个整数", "非法数字格式", JOptionPane.ERROR_MESSAGE ); } catch ( Exception dbze ) { JOptionPane.showMessageDialog( this, "除法异常", "除数为零", JOptionPane.ERROR_MESSAGE ); } } public double quotient( int numerator, int denominator ) throws Exception { if ( denominator == 0 ) throw new Exception(); return ( double ) numerator / denominator; } public static void main( String args[] ) { Java_3 app = new Java_3(); app.addWindowListener( new WindowAdapter() { public void windowClosing( WindowEvent e ) { e.getWindow().dispose(); System.exit( 0 ); } } ); } }四、关键知识点解析 1. Swing GUI编程 JFrame：顶级窗口容器 JTextField：文本输入框 JLabel：文本标签 GridLayout：网格布局管理器 JOptionPane：标准对话框 2. 异常处理机制 NumberFormatException：数字格式异常 自定义异常：通过throw new Exception()抛出 try-catch-finally：异常捕获处理结构 throws声明：方法可能抛出的异常 3. 事件处理模型 ActionListener接口：处理动作事件 addActionListener：注册事件监听器 actionPerformed：事件处理方法 五、常见错误分析 GUI组件初始化顺序错误： 先添加组件再设置布局 组件未添加到内容面板 异常捕获顺序不当： 更具体的异常应放在前面 Exception应放在最后 对话框参数顺序错误： showMessageDialog的参数顺序容易混淆 未处理窗口关闭事件： 需要添加WindowListener 否则点击关闭按钮不会退出程序 六、扩展思考 1. 改进用户体验 添加输入验证 支持键盘快捷键 增加计算历史记录 2. 异常处理最佳实践 自定义异常类（如DivideByZeroException） 异常日志记录 友好的错误提示 3. 多语言支持 使用资源束实现国际化： ResourceBundle bundle = ResourceBundle.getBundle("Messages"); String title = bundle.getString("window.title");七、考试技巧 先整体后局部：先理解程序整体结构再填空 注意上下文：填空处通常与上下文有直接关联 API文档记忆：记住常用Swing组件和异常类 边界测试：考虑各种输入情况（正常、异常、边界值） 八、模拟练习 题目：补全温度转换程序（摄氏转华氏） public class TempConverter extends JFrame implements ActionListener { private JTextField celsius, fahrenheit; public TempConverter() { super("温度转换"); //*********Found******** Container c = ___________(); c.setLayout(new GridLayout(2, 2)); c.add(new JLabel("摄氏温度", SwingConstants.RIGHT)); celsius = new JTextField(10); c.add(celsius); celsius.addActionListener(this); c.add(new JLabel("华氏温度", SwingConstants.RIGHT)); fahrenheit = new JTextField(10); c.add(fahrenheit); setSize(300, 100); setVisible(true); } public void actionPerformed(ActionEvent e) { try { //*********Found******** double c = Double._________(celsius.getText()); double f = c * 9 / 5 + 32; fahrenheit.setText(String.format("%.1f", f)); } catch (NumberFormatException ex) { JOptionPane.showMessageDialog(this, "请输入数字", "错误", JOptionPane.ERROR_MESSAGE); } } public static void main(String[] args) { new TempConverter(); } }答案： getContentPane parseDouble 九、总结 通过这道综合应用题，我们掌握了： Swing GUI程序的基本结构 异常处理机制的实现方式 事件驱动编程模型 Java二级考试中综合题的解题思路 关键点记忆： JFrame是顶级窗口容器 异常处理try-catch块结构 JOptionPane显示对话框 布局管理器使用GridLayout 希望这篇解析能帮助你在Java二级考试中顺利解决GUI和异常处理相关的题目！
-
Java二级考试简单应用题解析：随机数阶乘计算 Java二级考试简单应用题解析：随机数阶乘计算 在计算机等级考试二级Java的简单应用题中，经常会考察基础算法实现和流程控制语句的使用。本文将通过一道典型的阶乘计算题目，详细讲解解题思路、代码填空技巧以及相关知识点，帮助考生掌握这类题型的解答方法。 一、题目分析 6.png图片 题目要求 程序功能： 生成一个0到20之间的随机整数 计算并打印该整数的阶乘 在指定位置补全代码，不能修改已有代码 原代码结构 import java.util.Random; public class Java_2 { public static void main(String args[]){ Random random = new Random(); float x = random.nextFloat(); // 产生0.0与1.0之间的一个浮点数 int n = Math.round(20*x); // 构造20以内的一个整数 long f = 1; // 保存阶乘的结果 int k = 1; // 循环变量 //*********Found******** do{__________; k++; //*********Found******** }__________ System.out.println(n+"!= "+f); } }二、解题思路 1. 理解阶乘计算 阶乘定义：n! = 1 × 2 × 3 × ... × n 例如：5! = 1 × 2 × 3 × 4 × 5 = 120 特别地，0! = 1 2. 分析现有代码 已实现部分： 随机数生成（0-20） 变量初始化（f=1, k=1） 结果输出 需要补全部分： do-while循环体 循环条件 3. 确定算法逻辑 使用循环累乘计算阶乘： 初始化结果f=1 循环变量k从1开始 每次循环将f乘以k k递增 直到k超过n时停止 三、代码填空详解 第一个填空位置 do{__________; k++;需要填入：阶乘计算的核心操作，即累乘操作 正确答案：f *= k; 或 f = f * k; 解释： 这里需要实现阶乘的累乘过程 每次循环将当前结果f乘以循环变量k 复合赋值运算符*=简洁高效 第二个填空位置 }__________需要填入：do-while循环的继续条件 正确答案：while(k <= n); 解释： 循环应持续到k超过n为止 do-while循环至少执行一次，适合阶乘计算（包括0!=1的情况） 注意分号不能遗漏 四、完整正确代码 import java.util.Random; public class Java_2 { public static void main(String args[]){ Random random = new Random(); float x = random.nextFloat(); // 产生0.0与1.0之间的一个浮点数 int n = Math.round(20*x); // 构造20以内的一个整数 long f = 1; // 保存阶乘的结果 int k = 1; // 循环变量 //*********Found******** do{f *= k; k++; //*********Found******** }while(k <= n); System.out.println(n+"!= "+f); } }五、关键知识点解析 1. 随机数生成 Java中生成随机数的两种常用方式： // 方法1：使用Random类 Random random = new Random(); int n = random.nextInt(21); // 0-20的随机整数 // 方法2：使用Math.random() int n = (int)(Math.random() * 21);2. 阶乘算法实现 三种常见的阶乘实现方式： for循环实现： long f = 1; for(int i=1; i<=n; i++){ f *= i; } while循环实现： long f = 1; int k = 1; while(k <= n){ f *= k; k++; } 递归实现： public static long factorial(int n){ if(n <= 1) return 1; return n * factorial(n-1); } 3. 数据类型选择 为什么使用long：20! = 2432902008176640000，超出int范围(2^31-1≈21亿) 更大数值：如需计算更大阶乘，可使用BigInteger 六、常见错误分析 循环条件错误： while(k < n)：会少乘一次n while(k <= 0)：死循环 初始值错误： f初始化为0：所有结果都会是0 k初始化为0：会多乘一次0 数据类型不足： 使用int存储结果：20!会溢出 边界条件忽略： 未考虑n=0的情况（题目中n∈[0,20]） 七、扩展思考 1. 性能优化 预先计算并缓存阶乘结果（空间换时间） 使用尾递归优化（Java不支持自动优化，但可读性好） 2. 异常处理 增加输入验证： if(n < 0){ System.out.println("负数没有阶乘"); return; }3. 大数处理 使用BigInteger计算更大阶乘： import java.math.BigInteger; BigInteger f = BigInteger.ONE; for(int i=1; i<=n; i++){ f = f.multiply(BigInteger.valueOf(i)); }八、考试技巧 仔细阅读注释：填空位置通常有明确提示 分析变量用途：理解已有变量的作用（如f存结果，k是计数器） 注意分号：do-while循环最后必须有分号 测试边界值：0!和1!是常见测试点 检查数据类型：确认是否可能溢出 九、模拟练习 题目：补全计算斐波那契数列的程序 public class Java_3 { public static void main(String[] args) { int n = 10; // 计算前10项 int a = 1, b = 1; System.out.print(a + " " + b + " "); //*********Found******** for(int i=3; __________; i++){ int c = a + b; System.out.print(c + " "); //*********Found******** __________; b = c; } } }答案： i <= n a = b 十、总结 通过这道阶乘计算题，我们掌握了： Java随机数生成的常用方法 使用循环结构实现阶乘算法 数据类型的选择与溢出预防 do-while循环的语法特点 二级考试简单应用题的解题技巧 关键点记忆： 阶乘初始化f=1 循环条件k<=n 结果类型用long do-while结尾有分号 希望这篇解析能帮助你在Java二级考试中顺利解决此类题目！
-
堆数据结构深度解析：如何准确识别合法堆结构 堆数据结构深度解析：如何准确识别合法堆结构 在计算机等级考试二级Java的数据结构部分，堆（Heap）的概念和性质是重要考点。本文将通过一道典型的选择题，系统讲解堆的定义、特征以及判断方法，帮助考生掌握堆结构的核心知识。 一、题目回顾 题目内容： 5.png图片 下列各序列中不是堆的是______。 选项： A. (91,85,53,36,47,30,24,12) B. (91,85,53,47,36,30,24,12) C. (47,91,53,85,30,12,24,36) D. (91,85,53,47,30,12,24,36) 二、堆的基本概念解析 1. 什么是堆？ 堆是一种完全二叉树，具有以下性质： 大顶堆：每个节点的值都大于或等于其子节点的值 小顶堆：每个节点的值都小于或等于其子节点的值 2. 堆的存储方式 堆通常用数组来实现，对于数组中位置i的元素： 父节点位置：(i-1)/2 左子节点位置：2i+1 右子节点位置：2i+2 三、题目深度解析 判断堆的步骤： 确认堆类型：首先判断是大顶堆还是小顶堆（本题明显是大顶堆） 构建树结构：将序列还原为完全二叉树 验证堆性质：检查每个节点是否满足堆的条件 遍历检查：从最后一个非叶子节点开始向前检查 对各选项的分析： 选项A：(91,85,53,36,47,30,24,12) 树结构： 91 / \ 85 53 / \ / \ 36 47 30 24 / 12 验证： 91 ≥ 85, 91 ≥ 53 85 ≥ 36, 85 ≥ 47 53 ≥ 30, 53 ≥ 24 36 ≥ 12 结论：合法大顶堆 选项B：(91,85,53,47,36,30,24,12) 树结构： 91 / \ 85 53 / \ / \ 47 36 30 24 / 12 验证： 所有父节点均大于等于子节点 结论：合法大顶堆 选项C：(47,91,53,85,30,12,24,36) 树结构： 47 / \ 91 53 / \ / \ 85 30 12 24 / 36 验证： 47 ≱ 91（违反堆性质） 其他节点虽然满足，但根节点不满足 结论：不是合法堆 选项D：(91,85,53,47,30,12,24,36) 树结构： 91 / \ 85 53 / \ / \ 47 30 12 24 / 36 验证： 所有父节点均大于等于子节点 结论：合法大顶堆 四、常见错误分析 忽略根节点： 只检查部分节点而遗漏根节点的验证 树结构构建错误： 错误地将数组映射到树结构，导致验证错误 堆类型混淆： 混淆大顶堆和小顶堆的判断标准 部分满足即判断： 看到部分节点满足就认为整个结构是堆 五、相关知识扩展 1. 堆的操作 插入元素： 将新元素放到底部 向上调整（up-heap） 删除堆顶： 用最后一个元素替换堆顶 向下调整（down-heap） 建堆： 自底向上调整 时间复杂度O(n) 2. 堆的应用 堆排序： 时间复杂度O(n log n) 空间复杂度O(1) 优先队列： Java中的PriorityQueue就是基于堆实现 Top K问题： 使用堆高效解决最大/最小的K个元素问题 3. Java中的堆实现 // 默认是小顶堆 PriorityQueue<Integer> minHeap = new PriorityQueue<>(); // 创建大顶堆 PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a,b) -> b - a); // 添加元素 maxHeap.offer(10); maxHeap.offer(5); // 获取堆顶元素 int top = maxHeap.peek(); // 10六、解题技巧总结 树形图示法： 将数组转化为树形结构 直观验证堆性质 公式验证法： 对于数组索引i的元素： 大顶堆：arr[i] ≥ arr[2i+1] && arr[i] ≥ arr[2i+2] 小顶堆：arr[i] ≤ arr[2i+1] && arr[i] ≤ arr[2i+2] 排除法： 先快速排除明显不符合的选项 再仔细验证剩余选项 边界检查法： 特别注意根节点和叶子节点的检查 七、模拟练习题 题目1：以下哪个序列是小顶堆？ A. (10,20,15,30,40,25,50) B. (10,15,20,30,40,25,50) C. (10,20,15,25,40,30,50) D. (50,40,30,25,20,15,10) 答案分析： A：20 ≰ 15（违反） B：合法小顶堆 C：20 ≰ 15（违反） D：是大顶堆 正确答案是B。 题目2：将(50,30,20,15,10,8,16)调整为合法堆，需要交换哪些元素？ 答案：已经是合法大顶堆，无需交换。 八、备考建议 理解本质：掌握堆的完全二叉树性质和数组表示法 多画图：通过画图加深对堆结构的理解 代码实践：实现堆的基本操作（插入、删除、建堆） 对比学习：比较堆与其他树结构的区别 九、总结 通过这道题目，我们深入理解了： 堆的定义和两种类型（大顶堆/小顶堆） 堆的数组表示方法 如何验证一个序列是否是合法的堆 堆在Java中的实现和应用 关键结论： 选项C的序列不是合法的堆，是本题正确答案 判断堆的关键是验证每个节点的值与其子节点的关系 堆结构在优先队列和堆排序中有重要应用 掌握堆的知识不仅有助于应对考试，也为学习更高级的数据结构和算法打下坚实基础。在实际编程中，Java的PriorityQueue类提供了现成的堆实现，理解其原理能帮助我们更好地使用它。
-
排序算法时间复杂度深度解析：寻找最坏情况下的性能王者 排序算法时间复杂度深度解析：寻找最坏情况下的性能王者 在计算机等级考试二级Java的数据结构部分，排序算法的时间复杂度是必考的重点内容。本文将通过一道典型的选择题，全面解析常见排序算法在最坏情况下的时间复杂度，帮助考生掌握算法性能分析的核心方法。 一、题目回顾 题目内容： 4.png图片 下列排序方法中，最坏情况下时间复杂度最小的是______。 选项： A. 冒泡排序 B. 快速排序 C. 堆排序 D. 希尔排序 二、排序算法时间复杂度总览 在分析最坏情况前，我们先了解各排序算法的平均和最坏时间复杂度： 排序算法平均时间复杂度最坏时间复杂度空间复杂度稳定性冒泡排序O(n²)O(n²)O(1)稳定快速排序O(n log n)O(n²)O(log n)不稳定堆排序O(n log n)O(n log n)O(1)不稳定希尔排序O(n log n)O(n²)O(1)不稳定三、最坏情况深度解析 1. 冒泡排序（选项A） 最坏情况：输入序列完全逆序 时间复杂度：O(n²) 需要进行n-1轮比较 每轮比较n-i次（i为当前轮数） 总比较次数：n(n-1)/2 2. 快速排序（选项B） 最坏情况：每次选择的基准都是当前序列的最大或最小元素 时间复杂度：O(n²) 递归深度达到n层 每层需要进行O(n)次比较 常见场景： 已排序或逆序的输入 所有元素相同 3. 堆排序（选项C） 最坏情况：与输入顺序无关 时间复杂度：O(n log n) 建堆过程：O(n) 每次调整堆：O(log n) 共需调整n-1次 特点： 任何情况下都保持O(n log n) 不受输入数据分布影响 4. 希尔排序（选项D） 最坏情况：取决于增量序列的选择 时间复杂度： 使用希尔增量时：O(n²) 使用Hibbard增量时：O(n^(3/2)) 不确定性： 性能严重依赖增量序列的选择 没有公认的最优增量序列 四、选项对比与正确答案 对比各算法的最坏时间复杂度： 冒泡排序：O(n²) 快速排序：O(n²) 堆排序：O(n log n) 希尔排序：O(n²)（按最保守估计） 显然，堆排序在最坏情况下保持O(n log n)的性能，是四个选项中最好的，因此正确答案是C。 五、常见误区警示 混淆平均情况和最坏情况： 快速排序平均性能很好，但最坏情况很差 不能因为快速排序通常快就选择它 忽略算法稳定性： 虽然本题不考察稳定性，但要注意堆排序和快速排序是不稳定的 希尔排序的增量序列误区： 认为希尔排序总是优于O(n²)，实际上取决于增量选择 堆排序的误解： 认为建堆的O(n)时间复杂度是整个算法的复杂度 六、相关知识扩展 1. 其他排序算法的最坏情况 排序算法最坏时间复杂度插入排序O(n²)选择排序O(n²)归并排序O(n log n)计数排序O(n+k)基数排序O(d(n+k))桶排序O(n²)2. Java中的排序实现 Java的Arrays.sort()方法根据数据类型选择不同算法： 基本类型：快速排序变体（Dual-Pivot QuickSort） 对象类型：归并排序变体（TimSort） int[] arr = {5, 2, 9, 1, 5}; Arrays.sort(arr); // 最坏O(n log n) List<Integer> list = Arrays.asList(5, 2, 9, 1, 5); Collections.sort(list); // 最坏O(n log n)七、解题技巧总结 记忆法： 记住堆排序和归并排序的最坏O(n log n) 记住快速排序的最坏O(n²) 排除法： 先排除明显较差的选项 在剩余选项中比较 特性分析法： 分析各算法的特性决定其最坏情况 实际应用考量： 虽然堆排序最坏情况好，但实际应用中常数因子较大 快速排序通常更快，除非必须保证最坏情况性能 八、模拟练习题 题目1：以下排序算法中，平均和最坏时间复杂度均为O(n log n)的是？ A. 快速排序 B. 插入排序 C. 归并排序 D. 希尔排序 答案分析： 快速排序最坏O(n²) 插入排序最坏O(n²) 归并排序始终O(n log n) 希尔排序最坏O(n²) 正确答案是C。 题目2：对大量数据排序且要求最坏情况下性能稳定，应选用？ A. 冒泡排序 B. 快速排序 C. 堆排序 D. 希尔排序 正确答案是C。 九、备考建议 对比学习：制作对比表格记忆各算法特性 代码实现：亲手实现各排序算法加深理解 性能测试：对不同规模数据测试各算法实际性能 关注应用：了解Java标准库中的排序实现 十、总结 通过这道题目，我们深入理解了： 各排序算法在最坏情况下的性能表现 堆排序在最坏情况下仍保持O(n log n)的优势 快速排序在特定情况下性能会退化 算法选择需要权衡平均性能和最坏情况 关键结论： 堆排序是本题四个选项中最坏情况下时间复杂度最小的排序算法 实际应用中，算法选择需考虑数据特征、规模和要求 Java标准库根据数据类型智能选择排序算法 掌握这些知识不仅有助于应对考试，也为实际编程中的算法选择提供了理论依据。
-
深入解析线性结构的判定：从集合关系到数据结构选择 深入解析线性结构的判定：从集合关系到数据结构选择 在计算机等级考试二级Java的数据结构部分，理解线性结构的本质及其数学表示是重要考点。本文将通过一道典型的选择题，系统讲解如何通过关系R判断数据结构类型，帮助考生掌握线性结构的核心特征和判定方法。 一、题目回顾 题目内容： 3.png图片 设数据元素的集合D={1,2,3,4,5}，则满足下列关系R的数据结构中为线性结构的是______。 选项： A. R={(1,2),(3,2),(5,1),(4,5)} B. R={(1,3),(4,1),(3,2),(5,4)} C. R={(1,2),(2,4),(4,5),(2,3)} D. R={(1,3),(2,4),(3,5),(1,2)} 二、核心概念解析 1. 什么是线性结构？ 线性结构是指数据元素之间存在一对一的关系，具有以下特征： 唯一首元素：没有前驱的元素 唯一尾元素：没有后继的元素 中间元素：有且仅有一个前驱和一个后继 顺序性：元素按序排列，形成线性序列 常见线性结构：数组、链表、栈、队列等 2. 关系R的含义 题目中的关系R表示数据元素之间的前驱-后继关系。例如： (a,b)∈R 表示a是b的前驱，b是a的后继 通过R可以构建出完整的元素排列顺序 三、题目深度解析 判定线性结构的步骤： 检查首元素：找出没有前驱的元素（入度为0） 检查尾元素：找出没有后继的元素（出度为0） 检查中间元素：每个中间元素应有且仅有一个前驱和一个后继 验证连通性：所有元素应能连成一条线，无分叉 对各选项的分析： 选项A：R={(1,2),(3,2),(5,1),(4,5)} 图示关系： 3 → 2 4 → 5 → 1 → 2 问题：元素2有两个前驱（1和3），不符合线性结构要求 结论：非线性 选项B：R={(1,3),(4,1),(3,2),(5,4)} 图示关系： 5 → 4 → 1 → 3 → 2 特点： 首元素：5（无前驱） 尾元素：2（无后继） 每个中间元素只有一个前驱和一个后继 结论：线性结构（顺序：5→4→1→3→2） 选项C：R={(1,2),(2,4),(4,5),(2,3)} 图示关系： 1 → 2 → 4 → 5 ↘ 3 问题：元素2有两个后继（3和4），产生分叉 结论：非线性 选项D：R={(1,3),(2,4),(3,5),(1,2)} 图示关系： 1 → 3 → 5 ↓ 2 → 4 问题：元素1有两个后继（2和3），形成分叉 结论：非线性 四、常见错误分析 忽略唯一性要求： 认为只要元素能连成线就是线性结构（实际上必须严格一对一） 方向混淆： 将前驱和后继关系弄反（注意(a,b)表示a→b） 连通性检查不足： 没有发现存在孤立元素或未连接的元素 多路径误判： 忽略了一个元素有多个前驱或后继的情况 五、相关知识扩展 1. 其他数据结构类型的特征 树形结构： 有且仅有一个根节点 除根外每个节点有且仅有一个前驱 节点可以有多个后继 图状结构： 节点可以有任意数量的前驱和后继 包含环路也是可能的 集合结构： 元素之间没有特定的关系 2. 线性结构的Java实现 在Java中常见的线性结构实现： // 1. 数组（固定大小线性表） int[] array = new int[10]; // 2. ArrayList（动态数组） List<Integer> arrayList = new ArrayList<>(); // 3. LinkedList（链式实现） List<Integer> linkedList = new LinkedList<>(); // 4. Stack（栈，继承自Vector） Stack<Integer> stack = new Stack<>(); // 5. Queue（队列接口） Queue<Integer> queue = new LinkedList<>();六、解题技巧总结 图示法： 将关系R绘制成有向图 观察图形是否符合线性特征 度分析法： 计算每个元素的入度（前驱数量）和出度（后继数量） 线性结构应满足： 首元素：入度=0，出度=1 尾元素：入度=1，出度=0 中间元素：入度=1，出度=1 排除法： 先排除明显不符合的选项（如存在元素有多个前驱/后继） 验证法： 对可能的选项构建完整序列，验证连通性和唯一性 七、模拟练习题 题目：设D={a,b,c,d,e}，以下哪个关系R对应的数据结构是线性结构？ A. R={(a,b),(b,c),(d,e)} B. R={(a,b),(a,c),(b,d)} C. R={(a,b),(b,c),(c,d),(d,e)} D. R={(a,b),(c,b),(d,c)} 答案分析： A：不连通（a→b→c和d→e两部分） B：a有两个后继（分叉） C：完美线性（a→b→c→d→e） D：b有两个前驱 正确答案是C。 八、备考建议 掌握本质：理解线性结构的严格定义，不满足任一条件就不是线性结构 多画图：将抽象的关系转化为直观的图形表示 比较学习：对比线性、树形和图状结构的区别 代码实践：用Java实现各种数据结构，加深理解 九、总结 通过这道题目，我们深入理解了： 线性结构的严格定义和特征 如何通过关系R判断数据结构类型 使用图示法和度分析法解题的技巧 线性结构与其他数据结构的区别 关键记忆点： 线性结构要求严格的一对一关系 首尾元素具有特殊性 中间元素必须恰好一个前驱一个后继 Java集合框架提供了多种线性结构的实现 掌握这些知识不仅有助于应对考试，也为后续学习更复杂的数据结构和算法打下坚实基础。
