找到
685
篇与
阿贵
相关的结果
- 第 38 页
-
 Java输入流与条件求和实战解析:计算输入偶数的和 Java输入流与条件求和实战解析:计算输入偶数的和 一、原题完整代码呈现 29.png图片 以下是计算机二级Java考试中关于输入流处理和条件求和的典型题型,包含4处需要填写的空白(标记为//*********Found**********): //*********Found********** import java.______________.*; public class Java_1 { public static void main(String[ ] args) throws IOException { InputStreamReader ir; BufferedReader in; int sum, x; String data; //*********Found********** _______________; ir = new InputStreamReader(System.in); in = new BufferedReader(ir); System.out.println("请输入5个整数:"); //*********Found********** for (int i = 1; ____________; i++) { data = in.readLine(); x = Integer.parseInt(data); //*********Found********** if (___________) sum += x; } System.out.println("偶数之和为"+ sum ); } }二、空白处逐一解析与解答 1. 第一处空白:输入输出包导入 答案:io //*********Found********** import java.io.*;解析: 程序中使用了InputStreamReader和BufferedReader类,这些类属于Java的输入输出包java.io。通过import java.io.*;语句导入该包下的所有类,才能在程序中使用这些输入处理相关的类。 2. 第二处空白:初始化求和变量 答案:sum = 0 //*********Found********** sum = 0;解析: sum变量用于累加偶数的和,必须在使用前初始化。如果不初始化,Java会报编译错误(局部变量未初始化)。初始值设为0,确保累加从0开始。 3. 第三处空白:控制循环次数 答案:i <= 5 //*********Found********** for (int i = 1; i <= 5; i++) {解析: 题目要求输入5个整数,循环变量i从1开始计数,当i <= 5时继续循环,共执行5次,刚好接收5个输入值。 4. 第四处空白:判断偶数的条件 答案:x % 2 == 0 //*********Found********** if (x % 2 == 0) sum += x;解析: 一个数是偶数的判定标准是能被2整除,即除以2的余数为0。x % 2 == 0表示当x是偶数时,将其值累加到sum中。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现以下功能: 通过键盘接收用户输入的5个整数 筛选出其中的偶数并计算它们的总和 输出偶数之和的结果 运行说明 程序运行后,显示提示信息"请输入5个整数:" 用户需要依次输入5个整数,每次输入后按回车(例如:3、4、7、8、10) 程序会自动判断每个数是否为偶数,并累加偶数的和 输入完成后,输出结果(例如:"偶数之和为22",即4+8+10=22) 五、核心知识点总结 输入流处理 输入流链:System.in(标准输入字节流)→ InputStreamReader(字节转字符)→ BufferedReader(缓冲字符流) 读取方法:BufferedReader的readLine()方法用于读取一行文本输入 异常处理:readLine()可能抛出IOException,程序通过throws IOException声明抛出 类型转换 Integer.parseInt(String s):将输入的字符串转换为整数 注意事项:如果输入的不是合法整数,会抛出NumberFormatException 循环控制 循环次数:通过for (int i = 1; i <= 5; i++)精确控制输入5个数据 循环变量作用:i作为计数器,确保只接收指定数量的输入 偶数判断与累加 偶数判定:x % 2 == 0(取模运算结果为0表示能被2整除) 累加逻辑:sum += x等价于sum = sum + x,将符合条件的数累加到总和 六、常见错误与应试技巧 常见错误分析 第一处空白包名错误:写成input或ioStream,正确包名是io 第二处空白未初始化sum:局部变量必须初始化才能使用,否则编译报错 第三处循环条件错误:写成i < 5会导致只输入4个数据,不符合题目要求 第四处偶数判断错误:写成x % 2 = 0(赋值符号)或x % 2 != 0(判断奇数) 应试技巧 输入处理模板:记住BufferedReader in = new BufferedReader(new InputStreamReader(System.in));的标准写法 累加变量初始化:求和类问题中,累加变量(如sum)必须初始化为0 循环次数计算:从1开始计数时,循环条件i <= n确保执行n次 奇偶判断公式:偶数x % 2 == 0,奇数x % 2 != 0 通过本题,我们掌握了Java中键盘输入的处理流程、循环控制、条件判断和累加运算的综合应用。这类题目在实际开发中常用于数据统计、用户输入验证等场景,考察对基础语法和输入处理的掌握程度,是Java入门的重要知识点。
Java输入流与条件求和实战解析:计算输入偶数的和 Java输入流与条件求和实战解析:计算输入偶数的和 一、原题完整代码呈现 29.png图片 以下是计算机二级Java考试中关于输入流处理和条件求和的典型题型,包含4处需要填写的空白(标记为//*********Found**********): //*********Found********** import java.______________.*; public class Java_1 { public static void main(String[ ] args) throws IOException { InputStreamReader ir; BufferedReader in; int sum, x; String data; //*********Found********** _______________; ir = new InputStreamReader(System.in); in = new BufferedReader(ir); System.out.println("请输入5个整数:"); //*********Found********** for (int i = 1; ____________; i++) { data = in.readLine(); x = Integer.parseInt(data); //*********Found********** if (___________) sum += x; } System.out.println("偶数之和为"+ sum ); } }二、空白处逐一解析与解答 1. 第一处空白:输入输出包导入 答案:io //*********Found********** import java.io.*;解析: 程序中使用了InputStreamReader和BufferedReader类,这些类属于Java的输入输出包java.io。通过import java.io.*;语句导入该包下的所有类,才能在程序中使用这些输入处理相关的类。 2. 第二处空白:初始化求和变量 答案:sum = 0 //*********Found********** sum = 0;解析: sum变量用于累加偶数的和,必须在使用前初始化。如果不初始化,Java会报编译错误(局部变量未初始化)。初始值设为0,确保累加从0开始。 3. 第三处空白:控制循环次数 答案:i <= 5 //*********Found********** for (int i = 1; i <= 5; i++) {解析: 题目要求输入5个整数,循环变量i从1开始计数,当i <= 5时继续循环,共执行5次,刚好接收5个输入值。 4. 第四处空白:判断偶数的条件 答案:x % 2 == 0 //*********Found********** if (x % 2 == 0) sum += x;解析: 一个数是偶数的判定标准是能被2整除,即除以2的余数为0。x % 2 == 0表示当x是偶数时,将其值累加到sum中。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现以下功能: 通过键盘接收用户输入的5个整数 筛选出其中的偶数并计算它们的总和 输出偶数之和的结果 运行说明 程序运行后,显示提示信息"请输入5个整数:" 用户需要依次输入5个整数,每次输入后按回车(例如:3、4、7、8、10) 程序会自动判断每个数是否为偶数,并累加偶数的和 输入完成后,输出结果(例如:"偶数之和为22",即4+8+10=22) 五、核心知识点总结 输入流处理 输入流链:System.in(标准输入字节流)→ InputStreamReader(字节转字符)→ BufferedReader(缓冲字符流) 读取方法:BufferedReader的readLine()方法用于读取一行文本输入 异常处理:readLine()可能抛出IOException,程序通过throws IOException声明抛出 类型转换 Integer.parseInt(String s):将输入的字符串转换为整数 注意事项:如果输入的不是合法整数,会抛出NumberFormatException 循环控制 循环次数:通过for (int i = 1; i <= 5; i++)精确控制输入5个数据 循环变量作用:i作为计数器,确保只接收指定数量的输入 偶数判断与累加 偶数判定:x % 2 == 0(取模运算结果为0表示能被2整除) 累加逻辑:sum += x等价于sum = sum + x,将符合条件的数累加到总和 六、常见错误与应试技巧 常见错误分析 第一处空白包名错误:写成input或ioStream,正确包名是io 第二处空白未初始化sum:局部变量必须初始化才能使用,否则编译报错 第三处循环条件错误:写成i < 5会导致只输入4个数据,不符合题目要求 第四处偶数判断错误:写成x % 2 = 0(赋值符号)或x % 2 != 0(判断奇数) 应试技巧 输入处理模板:记住BufferedReader in = new BufferedReader(new InputStreamReader(System.in));的标准写法 累加变量初始化:求和类问题中,累加变量(如sum)必须初始化为0 循环次数计算:从1开始计数时,循环条件i <= n确保执行n次 奇偶判断公式:偶数x % 2 == 0,奇数x % 2 != 0 通过本题,我们掌握了Java中键盘输入的处理流程、循环控制、条件判断和累加运算的综合应用。这类题目在实际开发中常用于数据统计、用户输入验证等场景,考察对基础语法和输入处理的掌握程度,是Java入门的重要知识点。 -
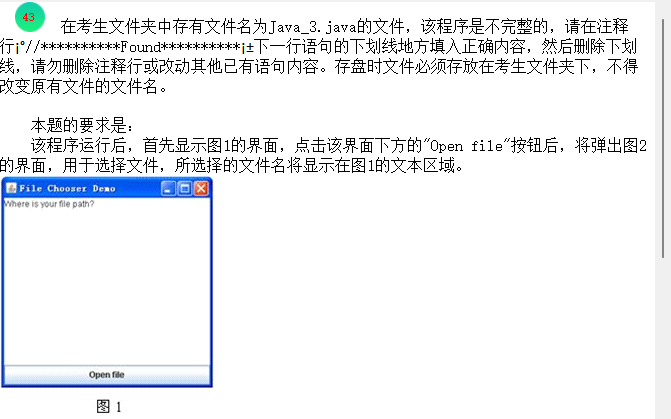
 Java Swing 文件选择器实战解析:实现文件选择功能 Java Swing 文件选择器实战解析:实现文件选择功能 一、原题完整代码呈现 27.png图片 28.png图片 以下是计算机二级Java考试中关于Swing文件选择器的典型题型,主要考察事件监听和文件选择对话框的使用,包含4处需要填写的空白(标记为//*********Found**********): import javax.swing.*; import java.awt.event.*; import java.io.*; import java.awt.*; //*********Found********** public class Java_3 implements ________________{ JFrame f; JTextArea ta; JFileChooser fc; Container c; File myFile; public static void main(String args[]){ Java_3 demo=new Java_3(); demo.go(); } void go(){ JFrame f=new JFrame("File Chooser Demo"); JButton b=new JButton("Open file"); ta=new JTextArea("Where is your file path?",10,30); //*********Found********** b.addActionListener(_________); c=f.getContentPane(); f.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); f.getContentPane().add("South",b); f.getContentPane().add("Center",ta); f.setSize(300,300); f.setVisible(true); } public void actionPerformed(ActionEvent e){ fc=new JFileChooser(); //*********Found********** int selected=fc.__________________(c); if (selected==JFileChooser.APPROVE_OPTION){ myFile=fc.getSelectedFile(); //*********Found********** ta.setText("You have selected file: "+myFile._____________()); } } }二、空白处逐一解析与解答 1. 第一处空白:实现事件监听接口 答案:ActionListener //*********Found********** public class Java_3 implements ActionListener{解析: 程序中需要处理按钮点击事件,ActionListener是Swing中处理动作事件的接口,包含actionPerformed(ActionEvent e)方法。类声明实现该接口后,才能重写事件处理方法,因此此处填写ActionListener。 2. 第二处空白:绑定事件监听器 答案:this //*********Found********** b.addActionListener(this);解析: JButton的addActionListener()方法需要接收一个ActionListener实例作为参数。当前类Java_3实现了ActionListener接口,this表示当前对象,因此将当前对象作为监听器绑定到按钮上,实现按钮点击事件的处理。 3. 第三处空白:显示文件选择对话框 答案:showOpenDialog //*********Found********** int selected=fc.showOpenDialog(c); 解析: JFileChooser的showOpenDialog(Component parent)方法用于显示"打开文件"对话框,参数为对话框的父组件。该方法返回用户的操作结果(如JFileChooser.APPROVE_OPTION表示用户选择了文件并点击了"打开"),因此此处填写showOpenDialog。 4. 第四处空白:获取选中文件的路径 答案:getAbsolutePath //*********Found********** ta.setText("You have selected file: "+myFile.getAbsolutePath());解析: File类的getAbsolutePath()方法用于返回文件的绝对路径。程序需要在文本区域中显示用户选中的文件路径,因此调用该方法获取路径字符串,填写getAbsolutePath。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现了一个简单的文件选择器功能,核心功能包括: 显示一个带有"Open file"按钮和文本区域的窗口 点击按钮时弹出文件选择对话框 用户选择文件后,在文本区域显示所选文件的绝对路径 运行说明 程序启动后,显示标题为"File Chooser Demo"的窗口,底部有"Open file"按钮,中间文本区域显示提示信息 点击"Open file"按钮,弹出文件选择对话框 在对话框中选择任意文件,点击"打开"按钮 文本区域会更新为"You have selected file: "加上所选文件的绝对路径 若点击对话框的"取消"按钮,则不做任何修改 五、核心知识点总结 事件监听机制 接口实现:通过implements ActionListener使类具备事件处理能力 方法重写:必须实现actionPerformed(ActionEvent e)方法处理具体事件 绑定关系:通过addActionListener(this)将组件与监听器关联 JFileChooser文件选择器 实例化:new JFileChooser()创建文件选择器对象 显示对话框: showOpenDialog(parent):显示"打开文件"对话框 showSaveDialog(parent):显示"保存文件"对话框 结果处理:返回值为JFileChooser.APPROVE_OPTION(确认)、CANCEL_OPTION(取消)等 Swing组件布局 容器获取:f.getContentPane()获取窗口的内容面板 组件添加:add(位置, 组件)方法添加组件到容器 "South":底部区域 "Center":中间区域 窗口设置:setSize()设置大小,setVisible(true)显示窗口 File类的常用方法 getAbsolutePath():返回文件的绝对路径 getName():返回文件名(不含路径) exists():判断文件是否存在 isFile():判断是否为文件(非目录) 六、常见错误与应试技巧 常见错误分析 第一处空白遗漏接口实现:忘记implements ActionListener会导致无法重写actionPerformed方法 第二处空白监听器绑定错误:误填new ActionListener()会创建匿名对象,但未实现方法体 第三处空白对话框方法错误:使用showDialog()而非showOpenDialog(),参数或返回值处理复杂 第四处空白文件方法错误:使用getPath()可能返回相对路径,而题目需要显示完整路径 应试技巧 事件监听模板:"实现接口→重写方法→绑定监听器"三步曲 文件选择器口诀:"new出选择器,showOpenDialog显窗口,APPROVE_OPTION判确认" 路径获取:需要完整路径用getAbsolutePath(),仅需文件名用getName() 组件添加:记住"North(上)、South(下)、East(右)、West(左)、Center(中)"的位置常量 通过本题,我们掌握了Swing中文件选择器的基本使用方法,包括事件监听的实现、文件对话框的显示和文件路径的获取。这些知识点在实际开发中广泛应用于需要用户选择文件的场景,如文本编辑器的"打开"功能、图片浏览器的文件选择等,也是计算机二级Java考试中GUI部分的重要考点。
Java Swing 文件选择器实战解析:实现文件选择功能 Java Swing 文件选择器实战解析:实现文件选择功能 一、原题完整代码呈现 27.png图片 28.png图片 以下是计算机二级Java考试中关于Swing文件选择器的典型题型,主要考察事件监听和文件选择对话框的使用,包含4处需要填写的空白(标记为//*********Found**********): import javax.swing.*; import java.awt.event.*; import java.io.*; import java.awt.*; //*********Found********** public class Java_3 implements ________________{ JFrame f; JTextArea ta; JFileChooser fc; Container c; File myFile; public static void main(String args[]){ Java_3 demo=new Java_3(); demo.go(); } void go(){ JFrame f=new JFrame("File Chooser Demo"); JButton b=new JButton("Open file"); ta=new JTextArea("Where is your file path?",10,30); //*********Found********** b.addActionListener(_________); c=f.getContentPane(); f.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); f.getContentPane().add("South",b); f.getContentPane().add("Center",ta); f.setSize(300,300); f.setVisible(true); } public void actionPerformed(ActionEvent e){ fc=new JFileChooser(); //*********Found********** int selected=fc.__________________(c); if (selected==JFileChooser.APPROVE_OPTION){ myFile=fc.getSelectedFile(); //*********Found********** ta.setText("You have selected file: "+myFile._____________()); } } }二、空白处逐一解析与解答 1. 第一处空白:实现事件监听接口 答案:ActionListener //*********Found********** public class Java_3 implements ActionListener{解析: 程序中需要处理按钮点击事件,ActionListener是Swing中处理动作事件的接口,包含actionPerformed(ActionEvent e)方法。类声明实现该接口后,才能重写事件处理方法,因此此处填写ActionListener。 2. 第二处空白:绑定事件监听器 答案:this //*********Found********** b.addActionListener(this);解析: JButton的addActionListener()方法需要接收一个ActionListener实例作为参数。当前类Java_3实现了ActionListener接口,this表示当前对象,因此将当前对象作为监听器绑定到按钮上,实现按钮点击事件的处理。 3. 第三处空白:显示文件选择对话框 答案:showOpenDialog //*********Found********** int selected=fc.showOpenDialog(c); 解析: JFileChooser的showOpenDialog(Component parent)方法用于显示"打开文件"对话框,参数为对话框的父组件。该方法返回用户的操作结果(如JFileChooser.APPROVE_OPTION表示用户选择了文件并点击了"打开"),因此此处填写showOpenDialog。 4. 第四处空白:获取选中文件的路径 答案:getAbsolutePath //*********Found********** ta.setText("You have selected file: "+myFile.getAbsolutePath());解析: File类的getAbsolutePath()方法用于返回文件的绝对路径。程序需要在文本区域中显示用户选中的文件路径,因此调用该方法获取路径字符串,填写getAbsolutePath。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现了一个简单的文件选择器功能,核心功能包括: 显示一个带有"Open file"按钮和文本区域的窗口 点击按钮时弹出文件选择对话框 用户选择文件后,在文本区域显示所选文件的绝对路径 运行说明 程序启动后,显示标题为"File Chooser Demo"的窗口,底部有"Open file"按钮,中间文本区域显示提示信息 点击"Open file"按钮,弹出文件选择对话框 在对话框中选择任意文件,点击"打开"按钮 文本区域会更新为"You have selected file: "加上所选文件的绝对路径 若点击对话框的"取消"按钮,则不做任何修改 五、核心知识点总结 事件监听机制 接口实现:通过implements ActionListener使类具备事件处理能力 方法重写:必须实现actionPerformed(ActionEvent e)方法处理具体事件 绑定关系:通过addActionListener(this)将组件与监听器关联 JFileChooser文件选择器 实例化:new JFileChooser()创建文件选择器对象 显示对话框: showOpenDialog(parent):显示"打开文件"对话框 showSaveDialog(parent):显示"保存文件"对话框 结果处理:返回值为JFileChooser.APPROVE_OPTION(确认)、CANCEL_OPTION(取消)等 Swing组件布局 容器获取:f.getContentPane()获取窗口的内容面板 组件添加:add(位置, 组件)方法添加组件到容器 "South":底部区域 "Center":中间区域 窗口设置:setSize()设置大小,setVisible(true)显示窗口 File类的常用方法 getAbsolutePath():返回文件的绝对路径 getName():返回文件名(不含路径) exists():判断文件是否存在 isFile():判断是否为文件(非目录) 六、常见错误与应试技巧 常见错误分析 第一处空白遗漏接口实现:忘记implements ActionListener会导致无法重写actionPerformed方法 第二处空白监听器绑定错误:误填new ActionListener()会创建匿名对象,但未实现方法体 第三处空白对话框方法错误:使用showDialog()而非showOpenDialog(),参数或返回值处理复杂 第四处空白文件方法错误:使用getPath()可能返回相对路径,而题目需要显示完整路径 应试技巧 事件监听模板:"实现接口→重写方法→绑定监听器"三步曲 文件选择器口诀:"new出选择器,showOpenDialog显窗口,APPROVE_OPTION判确认" 路径获取:需要完整路径用getAbsolutePath(),仅需文件名用getName() 组件添加:记住"North(上)、South(下)、East(右)、West(左)、Center(中)"的位置常量 通过本题,我们掌握了Swing中文件选择器的基本使用方法,包括事件监听的实现、文件对话框的显示和文件路径的获取。这些知识点在实际开发中广泛应用于需要用户选择文件的场景,如文本编辑器的"打开"功能、图片浏览器的文件选择等,也是计算机二级Java考试中GUI部分的重要考点。 -
 Java二维数组全方位解析:从基础到实战应用 Java二维数组全方位解析:从基础到实战应用 二维数组是Java中处理结构化数据的重要工具,广泛应用于矩阵运算、表格数据处理、游戏开发等场景。本文将从二维数组的基本概念出发,详细讲解其声明、初始化、访问方式,并通过实战案例展示其具体应用,帮助读者全面掌握二维数组的操作技巧。 一、二维数组的本质与内存结构 在Java中,二维数组本质上是"数组的数组",即一个数组中的每个元素都是另一个数组。这种结构决定了Java的二维数组不一定是规则的矩形,也可以是不规则的锯齿状结构。 从内存角度看,二维数组在内存中表现为: 外层数组(父数组)存储的是内层数组(子数组)的引用 每个子数组在内存中是独立存储的 子数组可以有不同的长度(锯齿状数组的特性) 二维数组内存结构示意图图片 图:Java二维数组的内存存储结构示意 二、二维数组的声明与初始化 2.1 声明方式 Java中二维数组有两种常用声明方式(推荐第一种): // 方式1:推荐使用,更清晰地表示二维数组 int[][] matrix1; // 方式2:与C语言类似,不推荐 int matrix2[][];2.2 初始化方法 2.2.1 静态初始化 直接指定数组元素的值,适用于已知初始数据的场景: // 声明的同时初始化 int[][] intMatrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }; // 不规则二维数组(锯齿数组) String[][] strMatrix = { {"a", "b"}, {"c"}, {"d", "e", "f"} };2.2.2 动态初始化 先指定数组长度,再为元素赋值,适用于初始数据未知的场景: // 方式1:同时指定外层和内层数组长度(规则矩阵) int[][] matrix = new int[3][4]; // 3行4列的整数矩阵 // 方式2:先指定外层长度,再分别初始化内层数组(灵活,可创建锯齿数组) int[][] jaggedMatrix = new int[3][]; jaggedMatrix[0] = new int[2]; // 第0行2列 jaggedMatrix[1] = new int[3]; // 第1行3列 jaggedMatrix[2] = new int[1]; // 第2行1列三、二维数组的基本操作 3.1 访问数组元素 通过双重索引访问二维数组中的元素,格式为数组名[行索引][列索引]: int[][] matrix = { {10, 20, 30}, {40, 50, 60} }; // 访问第1行第2列的元素(索引从0开始) int value = matrix[1][2]; // value = 60 // 修改第0行第1列的元素 matrix[0][1] = 200; // 矩阵变为{{10, 200, 30}, {40, 50, 60}}3.2 获取数组长度 外层数组长度(行数):数组名.length 内层数组长度(列数):数组名[行索引].length int[][] matrix = { {1, 2}, {3, 4, 5}, {6} }; System.out.println("行数:" + matrix.length); // 输出:3 System.out.println("第1行的列数:" + matrix[1].length); // 输出:33.3 遍历二维数组 遍历二维数组需要使用嵌套循环,外层循环遍历行,内层循环遍历列。 3.3.1 使用普通for循环 int[][] matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }; // 遍历二维数组 for (int i = 0; i < matrix.length; i++) { // 外层循环:行 for (int j = 0; j < matrix[i].length; j++) { // 内层循环:列 System.out.print(matrix[i][j] + " "); } System.out.println(); // 换行 }3.3.2 使用增强for循环(foreach) int[][] matrix = { {1, 2, 3}, {4, 5, 6} }; for (int[] row : matrix) { // 遍历每一行 for (int num : row) { // 遍历行中的每个元素 System.out.print(num + " "); } System.out.println(); }四、二维数组实战案例 4.1 案例1:创建并输出下三角矩阵 下三角矩阵是指主对角线以上的元素均为0的矩阵,以下代码展示了如何创建并格式化输出一个5×5的下三角矩阵: public class LowerTriangleMatrix { public static void main(String[] args) { int size = 5; int[][] matrix = new int[size][size]; int count = 1; // 填充下三角矩阵 for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { // 主对角线及以下区域填充递增数字,以上区域为0 if (j <= i) { matrix[i][j] = count++; } else { matrix[i][j] = 0; } } } // 格式化输出矩阵 System.out.println("5×5下三角矩阵:"); for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { // 控制输出格式,确保对齐 if (matrix[i][j] < 10) { System.out.print(matrix[i][j] + " "); } else { System.out.print(matrix[i][j] + " "); } } System.out.println(); // 换行 } } } 运行结果: 5×5下三角矩阵: 1 0 0 0 0 2 3 0 0 0 4 5 6 0 0 7 8 9 10 0 11 12 13 14 15 4.2 案例2:矩阵转置 矩阵转置是将矩阵的行和列进行交换的操作,以下代码实现了这一功能: public class MatrixTransposition { public static void main(String[] args) { // 原始矩阵 3行4列 int[][] original = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} }; // 计算转置矩阵的行和列 int rows = original.length; int cols = original[0].length; // 创建转置矩阵(行列互换) int[][] transposed = new int[cols][rows]; // 执行转置操作 for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { transposed[j][i] = original[i][j]; } } // 输出原始矩阵 System.out.println("原始矩阵(3×4):"); printMatrix(original); // 输出转置矩阵 System.out.println("转置矩阵(4×3):"); printMatrix(transposed); } // 打印矩阵的工具方法 private static void printMatrix(int[][] matrix) { for (int[] row : matrix) { for (int num : row) { System.out.print(num + "\t"); } System.out.println(); } } } 运行结果: 原始矩阵(3×4): 1 2 3 4 5 6 7 8 9 10 11 12 转置矩阵(4×3): 1 5 9 2 6 10 3 7 11 4 8 12 4.3 案例3:矩阵乘法 矩阵乘法是线性代数中的基本运算,要求第一个矩阵的列数等于第二个矩阵的行数,结果矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数: public class MatrixMultiplication { public static void main(String[] args) { // 矩阵A:2行3列 int[][] matrixA = { {1, 2, 3}, {4, 5, 6} }; // 矩阵B:3行2列(满足乘法条件:A的列数=B的行数) int[][] matrixB = { {7, 8}, {9, 10}, {11, 12} }; // 计算结果矩阵(2行2列) int[][] result = multiplyMatrices(matrixA, matrixB); // 输出结果 System.out.println("矩阵A × 矩阵B 的结果:"); printMatrix(result); } // 矩阵乘法实现 private static int[][] multiplyMatrices(int[][] a, int[][] b) { int aRows = a.length; int aCols = a[0].length; int bRows = b.length; int bCols = b[0].length; // 检查是否可以相乘(a的列数必须等于b的行数) if (aCols != bRows) { throw new IllegalArgumentException("矩阵A的列数必须等于矩阵B的行数"); } // 结果矩阵初始化 int[][] result = new int[aRows][bCols]; // 矩阵乘法核心逻辑 for (int i = 0; i < aRows; i++) { // 结果矩阵的行 for (int j = 0; j < bCols; j++) { // 结果矩阵的列 for (int k = 0; k < aCols; k++) { // 累加计算 result[i][j] += a[i][k] * b[k][j]; } } } return result; } // 打印矩阵 private static void printMatrix(int[][] matrix) { for (int[] row : matrix) { for (int num : row) { System.out.print(num + "\t"); } System.out.println(); } } } 运行结果: 矩阵A × 矩阵B 的结果: 58 64 139 154 五、二维数组常见错误与避坑指南 索引越界异常(ArrayIndexOutOfBoundsException) 原因:访问了超出数组长度的索引 避免:使用array.length和array[i].length控制循环范围 空指针异常(NullPointerException) 原因:访问了未初始化的内层数组 避免:动态初始化时确保所有内层数组都已正确初始化 锯齿数组的遍历问题 注意:不同行可能有不同的列数 解决:内层循环条件使用matrix[i].length而非固定值 数组复制误区 错误:直接使用array1 = array2(仅复制引用) 正确:使用双重循环逐个元素复制,或Arrays.copyOf()方法 六、总结与拓展 二维数组作为Java中处理结构化数据的重要工具,其核心操作包括声明初始化、元素访问、遍历和修改。通过本文的学习,我们掌握了: 二维数组的内存结构与本质(数组的数组) 多种声明和初始化方式的适用场景 嵌套循环在数组遍历中的应用 矩阵相关的实战案例(下三角矩阵、转置、乘法) 常见错误的避免方法 在实际开发中,二维数组常用于: 游戏开发中的地图表示(如棋盘、地形网格) 科学计算中的矩阵运算 数据分析中的表格数据处理 图像处理中的像素矩阵操作 掌握二维数组的操作是深入学习Java数据结构的基础,后续可以进一步学习ArrayList等集合框架,它们在处理动态二维数据时提供了更灵活的选择。
Java二维数组全方位解析:从基础到实战应用 Java二维数组全方位解析:从基础到实战应用 二维数组是Java中处理结构化数据的重要工具,广泛应用于矩阵运算、表格数据处理、游戏开发等场景。本文将从二维数组的基本概念出发,详细讲解其声明、初始化、访问方式,并通过实战案例展示其具体应用,帮助读者全面掌握二维数组的操作技巧。 一、二维数组的本质与内存结构 在Java中,二维数组本质上是"数组的数组",即一个数组中的每个元素都是另一个数组。这种结构决定了Java的二维数组不一定是规则的矩形,也可以是不规则的锯齿状结构。 从内存角度看,二维数组在内存中表现为: 外层数组(父数组)存储的是内层数组(子数组)的引用 每个子数组在内存中是独立存储的 子数组可以有不同的长度(锯齿状数组的特性) 二维数组内存结构示意图图片 图:Java二维数组的内存存储结构示意 二、二维数组的声明与初始化 2.1 声明方式 Java中二维数组有两种常用声明方式(推荐第一种): // 方式1:推荐使用,更清晰地表示二维数组 int[][] matrix1; // 方式2:与C语言类似,不推荐 int matrix2[][];2.2 初始化方法 2.2.1 静态初始化 直接指定数组元素的值,适用于已知初始数据的场景: // 声明的同时初始化 int[][] intMatrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }; // 不规则二维数组(锯齿数组) String[][] strMatrix = { {"a", "b"}, {"c"}, {"d", "e", "f"} };2.2.2 动态初始化 先指定数组长度,再为元素赋值,适用于初始数据未知的场景: // 方式1:同时指定外层和内层数组长度(规则矩阵) int[][] matrix = new int[3][4]; // 3行4列的整数矩阵 // 方式2:先指定外层长度,再分别初始化内层数组(灵活,可创建锯齿数组) int[][] jaggedMatrix = new int[3][]; jaggedMatrix[0] = new int[2]; // 第0行2列 jaggedMatrix[1] = new int[3]; // 第1行3列 jaggedMatrix[2] = new int[1]; // 第2行1列三、二维数组的基本操作 3.1 访问数组元素 通过双重索引访问二维数组中的元素,格式为数组名[行索引][列索引]: int[][] matrix = { {10, 20, 30}, {40, 50, 60} }; // 访问第1行第2列的元素(索引从0开始) int value = matrix[1][2]; // value = 60 // 修改第0行第1列的元素 matrix[0][1] = 200; // 矩阵变为{{10, 200, 30}, {40, 50, 60}}3.2 获取数组长度 外层数组长度(行数):数组名.length 内层数组长度(列数):数组名[行索引].length int[][] matrix = { {1, 2}, {3, 4, 5}, {6} }; System.out.println("行数:" + matrix.length); // 输出:3 System.out.println("第1行的列数:" + matrix[1].length); // 输出:33.3 遍历二维数组 遍历二维数组需要使用嵌套循环,外层循环遍历行,内层循环遍历列。 3.3.1 使用普通for循环 int[][] matrix = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }; // 遍历二维数组 for (int i = 0; i < matrix.length; i++) { // 外层循环:行 for (int j = 0; j < matrix[i].length; j++) { // 内层循环:列 System.out.print(matrix[i][j] + " "); } System.out.println(); // 换行 }3.3.2 使用增强for循环(foreach) int[][] matrix = { {1, 2, 3}, {4, 5, 6} }; for (int[] row : matrix) { // 遍历每一行 for (int num : row) { // 遍历行中的每个元素 System.out.print(num + " "); } System.out.println(); }四、二维数组实战案例 4.1 案例1:创建并输出下三角矩阵 下三角矩阵是指主对角线以上的元素均为0的矩阵,以下代码展示了如何创建并格式化输出一个5×5的下三角矩阵: public class LowerTriangleMatrix { public static void main(String[] args) { int size = 5; int[][] matrix = new int[size][size]; int count = 1; // 填充下三角矩阵 for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { // 主对角线及以下区域填充递增数字,以上区域为0 if (j <= i) { matrix[i][j] = count++; } else { matrix[i][j] = 0; } } } // 格式化输出矩阵 System.out.println("5×5下三角矩阵:"); for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { // 控制输出格式,确保对齐 if (matrix[i][j] < 10) { System.out.print(matrix[i][j] + " "); } else { System.out.print(matrix[i][j] + " "); } } System.out.println(); // 换行 } } } 运行结果: 5×5下三角矩阵: 1 0 0 0 0 2 3 0 0 0 4 5 6 0 0 7 8 9 10 0 11 12 13 14 15 4.2 案例2:矩阵转置 矩阵转置是将矩阵的行和列进行交换的操作,以下代码实现了这一功能: public class MatrixTransposition { public static void main(String[] args) { // 原始矩阵 3行4列 int[][] original = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} }; // 计算转置矩阵的行和列 int rows = original.length; int cols = original[0].length; // 创建转置矩阵(行列互换) int[][] transposed = new int[cols][rows]; // 执行转置操作 for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { transposed[j][i] = original[i][j]; } } // 输出原始矩阵 System.out.println("原始矩阵(3×4):"); printMatrix(original); // 输出转置矩阵 System.out.println("转置矩阵(4×3):"); printMatrix(transposed); } // 打印矩阵的工具方法 private static void printMatrix(int[][] matrix) { for (int[] row : matrix) { for (int num : row) { System.out.print(num + "\t"); } System.out.println(); } } } 运行结果: 原始矩阵(3×4): 1 2 3 4 5 6 7 8 9 10 11 12 转置矩阵(4×3): 1 5 9 2 6 10 3 7 11 4 8 12 4.3 案例3:矩阵乘法 矩阵乘法是线性代数中的基本运算,要求第一个矩阵的列数等于第二个矩阵的行数,结果矩阵的行数等于第一个矩阵的行数,列数等于第二个矩阵的列数: public class MatrixMultiplication { public static void main(String[] args) { // 矩阵A:2行3列 int[][] matrixA = { {1, 2, 3}, {4, 5, 6} }; // 矩阵B:3行2列(满足乘法条件:A的列数=B的行数) int[][] matrixB = { {7, 8}, {9, 10}, {11, 12} }; // 计算结果矩阵(2行2列) int[][] result = multiplyMatrices(matrixA, matrixB); // 输出结果 System.out.println("矩阵A × 矩阵B 的结果:"); printMatrix(result); } // 矩阵乘法实现 private static int[][] multiplyMatrices(int[][] a, int[][] b) { int aRows = a.length; int aCols = a[0].length; int bRows = b.length; int bCols = b[0].length; // 检查是否可以相乘(a的列数必须等于b的行数) if (aCols != bRows) { throw new IllegalArgumentException("矩阵A的列数必须等于矩阵B的行数"); } // 结果矩阵初始化 int[][] result = new int[aRows][bCols]; // 矩阵乘法核心逻辑 for (int i = 0; i < aRows; i++) { // 结果矩阵的行 for (int j = 0; j < bCols; j++) { // 结果矩阵的列 for (int k = 0; k < aCols; k++) { // 累加计算 result[i][j] += a[i][k] * b[k][j]; } } } return result; } // 打印矩阵 private static void printMatrix(int[][] matrix) { for (int[] row : matrix) { for (int num : row) { System.out.print(num + "\t"); } System.out.println(); } } } 运行结果: 矩阵A × 矩阵B 的结果: 58 64 139 154 五、二维数组常见错误与避坑指南 索引越界异常(ArrayIndexOutOfBoundsException) 原因:访问了超出数组长度的索引 避免:使用array.length和array[i].length控制循环范围 空指针异常(NullPointerException) 原因:访问了未初始化的内层数组 避免:动态初始化时确保所有内层数组都已正确初始化 锯齿数组的遍历问题 注意:不同行可能有不同的列数 解决:内层循环条件使用matrix[i].length而非固定值 数组复制误区 错误:直接使用array1 = array2(仅复制引用) 正确:使用双重循环逐个元素复制,或Arrays.copyOf()方法 六、总结与拓展 二维数组作为Java中处理结构化数据的重要工具,其核心操作包括声明初始化、元素访问、遍历和修改。通过本文的学习,我们掌握了: 二维数组的内存结构与本质(数组的数组) 多种声明和初始化方式的适用场景 嵌套循环在数组遍历中的应用 矩阵相关的实战案例(下三角矩阵、转置、乘法) 常见错误的避免方法 在实际开发中,二维数组常用于: 游戏开发中的地图表示(如棋盘、地形网格) 科学计算中的矩阵运算 数据分析中的表格数据处理 图像处理中的像素矩阵操作 掌握二维数组的操作是深入学习Java数据结构的基础,后续可以进一步学习ArrayList等集合框架,它们在处理动态二维数据时提供了更灵活的选择。 -
 Java二维数组初始化与格式化输出实战解析:下三角矩阵的创建 Java二维数组初始化与格式化输出实战解析:下三角矩阵的创建 一、原题完整代码呈现 25.png图片 以下是计算机二级Java考试中关于二维数组操作的典型题型,主要考察数组初始化和条件输出,包含4处需要填写的空白(标记为//*********Found**********): import java.io.*; public class Java_2{ public static void main(String args[]) { int a[][] = new int[5][5]; int i,j,k=1; for(i=0;i<5;i++) //*********Found********** for( j=0; _____________ ;j++ ) //*********Found********** if((i+j)< _________________) a[i][j]=0; else{ //*********Found********** _______________________; } for(i=0;i<5;i++){ for(j=0;j<5;j++) //*********Found********** if(a[i][j]< _________________) System.out.print(a[i][j]+ " "); else System.out.print(a[i][j]+ " "); System.out.println(); } } }二、空白处逐一解析与解答 1. 第一处空白:内层循环条件 答案:j < 5 //*********Found********** for( j=0; j < 5 ;j++ )解析: 程序创建了5×5的二维数组(int a[][] = new int[5][5]),内层循环用于遍历列索引。列索引j的有效范围是0~4(共5列),因此循环条件应为j < 5,确保遍历数组的每一列。 2. 第二处空白:三角区域判断阈值 答案:5 //*********Found********** if((i+j)< 5)解析: 条件(i+j) < 5用于区分数组的上三角和下三角区域。对于5×5的数组,当行索引i与列索引j之和小于5时,属于上三角区域(赋值为0);之和大于等于5时,属于下三角区域(赋递增数值),这是创建下三角矩阵的典型逻辑。 3. 第三处空白:下三角区域赋值 答案:a[i][j] = k++ //*********Found********** a[i][j] = k++;解析: k作为计数器初始值为1,下三角区域((i+j)≥5)需要填充递增的数值。a[i][j] = k++表示先将k的值赋给数组元素,再将k自增,确保每个下三角元素的值依次递增。 4. 第四处空白:格式化输出判断条件 答案:10 //*********Found********** if(a[i][j]< 10)解析: 输出时通过判断元素是否小于10来控制空格数量:小于10的元素后加3个空格,大于等于10的元素后加2个空格,使输出的矩阵对齐美观。由于数组元素最大为10(5×5矩阵的下三角元素共10个),因此判断阈值为10。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序运行结果与矩阵结构解析 运行结果 0 0 0 0 0 0 0 0 0 1 0 0 0 2 3 0 0 4 5 6 0 7 8 9 10 矩阵结构解析 程序创建了一个5×5的下三角矩阵,其结构特点如下: 上三角区域(i+j < 5):元素值均为0,包括: 第0行:所有元素(0+0=0至0+4=4均小于5) 第1行:前4列(1+0=1至1+3=4均小于5) 第2行:前3列(2+0=2至2+2=4均小于5) 第3行:前2列(3+0=3至3+1=4均小于5) 第4行:第0列(4+0=4小于5) 下三角区域(i+j ≥ 5):元素值从1开始递增,共10个元素: 第1行第4列:1(1+4=5) 第2行第3-4列:2、3 第3行第2-4列:4、5、6 第4行第1-4列:7、8、9、10 五、核心知识点总结 二维数组的遍历 嵌套循环结构:外层循环控制行(i),内层循环控制列(j) 循环条件:对于n×n的数组,行和列的循环条件均为索引 < n 索引范围:行索引和列索引均从0开始,最大索引为n-1 矩阵区域划分 上三角与下三角的判断:通过i+j < n(n为矩阵阶数)区分 赋值逻辑:根据区域特征设置不同值(上三角为0,下三角为递增数) 计数器应用:使用k++实现下三角区域的递增赋值 格式化输出技巧 条件判断:通过元素值大小(a[i][j] < 10)控制空格数量 对齐效果:一位数后加3个空格,两位数后加2个空格,使矩阵列对齐 换行控制:每行输出完毕后用println()换行 循环与条件结合 循环嵌套条件判断是处理二维数组的常用模式 先判断区域特征,再执行对应赋值操作,逻辑清晰易读 六、常见错误与应试技巧 常见错误分析 第一处空白循环条件错误:写成j <= 5会导致索引越界(最大索引为4) 第二处空白阈值错误:写成4会导致三角区域划分错误,影响矩阵结构 第三处空白赋值错误:写成a[i][j] = ++k会使起始值为2,破坏递增序列 第四处空白判断条件错误:写成9会导致10也使用3个空格,破坏对齐 应试技巧 数组遍历公式:for(i=0;i<n;i++) for(j=0;j<n;j++)是n×n数组的标准遍历模板 三角区域判断:记住i+j < n是n阶矩阵上三角的判断条件 递增赋值:k++实现先赋值后递增,适合从1开始的序列 格式化输出:根据元素位数差异设置不同空格数,确保对齐美观 通过本题,我们掌握了二维数组的区域划分、条件赋值和格式化输出的综合应用。这类题目在实际开发中常用于矩阵运算、数据可视化等场景,考察对嵌套循环和条件判断的灵活运用能力,也是计算机二级Java考试的重点题型。理解矩阵的索引特征和区域划分逻辑,对处理复杂的二维数据结构具有重要意义。
Java二维数组初始化与格式化输出实战解析:下三角矩阵的创建 Java二维数组初始化与格式化输出实战解析:下三角矩阵的创建 一、原题完整代码呈现 25.png图片 以下是计算机二级Java考试中关于二维数组操作的典型题型,主要考察数组初始化和条件输出,包含4处需要填写的空白(标记为//*********Found**********): import java.io.*; public class Java_2{ public static void main(String args[]) { int a[][] = new int[5][5]; int i,j,k=1; for(i=0;i<5;i++) //*********Found********** for( j=0; _____________ ;j++ ) //*********Found********** if((i+j)< _________________) a[i][j]=0; else{ //*********Found********** _______________________; } for(i=0;i<5;i++){ for(j=0;j<5;j++) //*********Found********** if(a[i][j]< _________________) System.out.print(a[i][j]+ " "); else System.out.print(a[i][j]+ " "); System.out.println(); } } }二、空白处逐一解析与解答 1. 第一处空白:内层循环条件 答案:j < 5 //*********Found********** for( j=0; j < 5 ;j++ )解析: 程序创建了5×5的二维数组(int a[][] = new int[5][5]),内层循环用于遍历列索引。列索引j的有效范围是0~4(共5列),因此循环条件应为j < 5,确保遍历数组的每一列。 2. 第二处空白:三角区域判断阈值 答案:5 //*********Found********** if((i+j)< 5)解析: 条件(i+j) < 5用于区分数组的上三角和下三角区域。对于5×5的数组,当行索引i与列索引j之和小于5时,属于上三角区域(赋值为0);之和大于等于5时,属于下三角区域(赋递增数值),这是创建下三角矩阵的典型逻辑。 3. 第三处空白:下三角区域赋值 答案:a[i][j] = k++ //*********Found********** a[i][j] = k++;解析: k作为计数器初始值为1,下三角区域((i+j)≥5)需要填充递增的数值。a[i][j] = k++表示先将k的值赋给数组元素,再将k自增,确保每个下三角元素的值依次递增。 4. 第四处空白:格式化输出判断条件 答案:10 //*********Found********** if(a[i][j]< 10)解析: 输出时通过判断元素是否小于10来控制空格数量:小于10的元素后加3个空格,大于等于10的元素后加2个空格,使输出的矩阵对齐美观。由于数组元素最大为10(5×5矩阵的下三角元素共10个),因此判断阈值为10。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序运行结果与矩阵结构解析 运行结果 0 0 0 0 0 0 0 0 0 1 0 0 0 2 3 0 0 4 5 6 0 7 8 9 10 矩阵结构解析 程序创建了一个5×5的下三角矩阵,其结构特点如下: 上三角区域(i+j < 5):元素值均为0,包括: 第0行:所有元素(0+0=0至0+4=4均小于5) 第1行:前4列(1+0=1至1+3=4均小于5) 第2行:前3列(2+0=2至2+2=4均小于5) 第3行:前2列(3+0=3至3+1=4均小于5) 第4行:第0列(4+0=4小于5) 下三角区域(i+j ≥ 5):元素值从1开始递增,共10个元素: 第1行第4列:1(1+4=5) 第2行第3-4列:2、3 第3行第2-4列:4、5、6 第4行第1-4列:7、8、9、10 五、核心知识点总结 二维数组的遍历 嵌套循环结构:外层循环控制行(i),内层循环控制列(j) 循环条件:对于n×n的数组,行和列的循环条件均为索引 < n 索引范围:行索引和列索引均从0开始,最大索引为n-1 矩阵区域划分 上三角与下三角的判断:通过i+j < n(n为矩阵阶数)区分 赋值逻辑:根据区域特征设置不同值(上三角为0,下三角为递增数) 计数器应用:使用k++实现下三角区域的递增赋值 格式化输出技巧 条件判断:通过元素值大小(a[i][j] < 10)控制空格数量 对齐效果:一位数后加3个空格,两位数后加2个空格,使矩阵列对齐 换行控制:每行输出完毕后用println()换行 循环与条件结合 循环嵌套条件判断是处理二维数组的常用模式 先判断区域特征,再执行对应赋值操作,逻辑清晰易读 六、常见错误与应试技巧 常见错误分析 第一处空白循环条件错误:写成j <= 5会导致索引越界(最大索引为4) 第二处空白阈值错误:写成4会导致三角区域划分错误,影响矩阵结构 第三处空白赋值错误:写成a[i][j] = ++k会使起始值为2,破坏递增序列 第四处空白判断条件错误:写成9会导致10也使用3个空格,破坏对齐 应试技巧 数组遍历公式:for(i=0;i<n;i++) for(j=0;j<n;j++)是n×n数组的标准遍历模板 三角区域判断:记住i+j < n是n阶矩阵上三角的判断条件 递增赋值:k++实现先赋值后递增,适合从1开始的序列 格式化输出:根据元素位数差异设置不同空格数,确保对齐美观 通过本题,我们掌握了二维数组的区域划分、条件赋值和格式化输出的综合应用。这类题目在实际开发中常用于矩阵运算、数据可视化等场景,考察对嵌套循环和条件判断的灵活运用能力,也是计算机二级Java考试的重点题型。理解矩阵的索引特征和区域划分逻辑,对处理复杂的二维数据结构具有重要意义。 -
 Java输入输出与闰年判断实战解析:键盘输入处理与条件判断 Java输入输出与闰年判断实战解析:键盘输入处理与条件判断 一、原题完整代码呈现 24.png图片 以下是计算机二级Java考试中关于键盘输入和闰年判断的典型题型,包含4处需要填写的空白(标记为//*********Found**********): //*********Found********** import java.____________.*; public class Java_1{ //*********Found********** public static void main(String[] args) ____________ Exception{ InputStreamReader ir; BufferedReader in; ir=new InputStreamReader(System.in); in=new BufferedReader(ir); System.out.println("输入年份是:"); //*********Found********** String s=____________.readLine(); //*********Found********** int year=Integer.parseInt(_____________); if(year%4==0&&year%100!=0||year%400==0){ System.out.println(""+year+"年是闰年."); } else{ System.out.println(""+year+"年不是闰年."); } } }二、空白处逐一解析与解答 1. 第一处空白:输入输出包导入 答案:io //*********Found********** import java.io.*;解析: 程序中使用了InputStreamReader和BufferedReader类,这些类属于Java的输入输出包java.io。import java.io.*;语句用于导入该包下的所有类,使程序能够识别这些输入处理相关的类。 2. 第二处空白:异常声明 答案:throws //*********Found********** public static void main(String[] args) throws Exception{解析: BufferedReader的readLine()方法会抛出IOException,这是一种已检查异常。处理异常的方式有两种:使用try-catch块捕获,或在方法声明中用throws关键字声明抛出。本题采用后者,因此填写throws。 3. 第三处空白:读取输入的对象 答案:in //*********Found********** String s=in.readLine();解析: 前面已经创建了BufferedReader对象in(in=new BufferedReader(ir);),BufferedReader的readLine()方法用于读取一行文本输入。因此此处应通过in对象调用该方法,将读取的字符串存储到s变量中。 4. 第四处空白:字符串转整数的参数 答案:s //*********Found********** int year=Integer.parseInt(s);解析: Integer.parseInt(String s)方法用于将字符串转换为整数。前面已经通过readLine()将用户输入的年份读取到字符串变量s中,此处需要将s作为参数传入,转换为整数类型的year变量,以便进行闰年判断。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现以下功能: 通过键盘接收用户输入的年份(字符串形式) 将输入的字符串转换为整数 根据闰年判断规则,判断该年份是否为闰年 输出判断结果 运行说明 程序运行后,会显示提示信息"输入年份是:" 用户需要输入一个整数年份(如2020、2023等)并按回车 程序会自动判断该年份是否为闰年,并输出结果: 闰年输出:"XXXX年是闰年." 非闰年输出:"XXXX年不是闰年." 五、核心知识点总结 输入处理流 InputStreamReader:将字节流(System.in)转换为字符流 BufferedReader:提供缓冲功能,其readLine()方法可读取一行文本 流的嵌套关系:System.in → InputStreamReader → BufferedReader,形成处理链 异常处理方式 声明抛出:在方法签名中用throws Exception声明可能抛出的异常 捕获处理:使用try-catch块捕获并处理异常 本题采用声明抛出方式,简化了代码结构(实际开发中更推荐try-catch) 类型转换 Integer.parseInt(String s):将字符串转换为整数 注意事项:如果字符串不是合法的整数格式,会抛出NumberFormatException 闰年判断规则 能被4整除但不能被100整除,或者能被400整除的年份是闰年 逻辑表达式:year%4==0&&year%100!=0||year%400==0 优先级说明:&& 优先级高于 ||,确保判断逻辑正确 六、常见错误与应试技巧 常见错误分析 第一处空白写错包名:如input或output,正确包名是io 第二处空白使用throw而非throws:throw用于抛出具体异常对象,throws用于方法声明 第三处空白用ir调用readLine():InputStreamReader没有readLine()方法,需通过BufferedReader对象in调用 第四处空白直接写字符串:如"s",应传入变量s而非字符串字面量 应试技巧 IO包记忆:输入输出相关类都在java.io包中 输入流链模板:BufferedReader in = new BufferedReader(new InputStreamReader(System.in)); 类型转换口诀:字符串转整数用Integer.parseInt(字符串变量) 闰年规则:记住"四年一闰,百年不闰,四百年再闰"的判断逻辑 通过本题,我们掌握了Java中键盘输入的处理方法、字符串与整数的类型转换,以及闰年判断的逻辑实现。这些知识点在实际开发中常用于数据输入、格式转换和业务逻辑判断,是Java基础编程的重要组成部分,也是计算机二级Java考试的常见考点。
Java输入输出与闰年判断实战解析:键盘输入处理与条件判断 Java输入输出与闰年判断实战解析:键盘输入处理与条件判断 一、原题完整代码呈现 24.png图片 以下是计算机二级Java考试中关于键盘输入和闰年判断的典型题型,包含4处需要填写的空白(标记为//*********Found**********): //*********Found********** import java.____________.*; public class Java_1{ //*********Found********** public static void main(String[] args) ____________ Exception{ InputStreamReader ir; BufferedReader in; ir=new InputStreamReader(System.in); in=new BufferedReader(ir); System.out.println("输入年份是:"); //*********Found********** String s=____________.readLine(); //*********Found********** int year=Integer.parseInt(_____________); if(year%4==0&&year%100!=0||year%400==0){ System.out.println(""+year+"年是闰年."); } else{ System.out.println(""+year+"年不是闰年."); } } }二、空白处逐一解析与解答 1. 第一处空白:输入输出包导入 答案:io //*********Found********** import java.io.*;解析: 程序中使用了InputStreamReader和BufferedReader类,这些类属于Java的输入输出包java.io。import java.io.*;语句用于导入该包下的所有类,使程序能够识别这些输入处理相关的类。 2. 第二处空白:异常声明 答案:throws //*********Found********** public static void main(String[] args) throws Exception{解析: BufferedReader的readLine()方法会抛出IOException,这是一种已检查异常。处理异常的方式有两种:使用try-catch块捕获,或在方法声明中用throws关键字声明抛出。本题采用后者,因此填写throws。 3. 第三处空白:读取输入的对象 答案:in //*********Found********** String s=in.readLine();解析: 前面已经创建了BufferedReader对象in(in=new BufferedReader(ir);),BufferedReader的readLine()方法用于读取一行文本输入。因此此处应通过in对象调用该方法,将读取的字符串存储到s变量中。 4. 第四处空白:字符串转整数的参数 答案:s //*********Found********** int year=Integer.parseInt(s);解析: Integer.parseInt(String s)方法用于将字符串转换为整数。前面已经通过readLine()将用户输入的年份读取到字符串变量s中,此处需要将s作为参数传入,转换为整数类型的year变量,以便进行闰年判断。 三、完整正确代码 隐藏内容,请前往内页查看详情 四、程序功能与运行说明 程序功能 该程序实现以下功能: 通过键盘接收用户输入的年份(字符串形式) 将输入的字符串转换为整数 根据闰年判断规则,判断该年份是否为闰年 输出判断结果 运行说明 程序运行后,会显示提示信息"输入年份是:" 用户需要输入一个整数年份(如2020、2023等)并按回车 程序会自动判断该年份是否为闰年,并输出结果: 闰年输出:"XXXX年是闰年." 非闰年输出:"XXXX年不是闰年." 五、核心知识点总结 输入处理流 InputStreamReader:将字节流(System.in)转换为字符流 BufferedReader:提供缓冲功能,其readLine()方法可读取一行文本 流的嵌套关系:System.in → InputStreamReader → BufferedReader,形成处理链 异常处理方式 声明抛出:在方法签名中用throws Exception声明可能抛出的异常 捕获处理:使用try-catch块捕获并处理异常 本题采用声明抛出方式,简化了代码结构(实际开发中更推荐try-catch) 类型转换 Integer.parseInt(String s):将字符串转换为整数 注意事项:如果字符串不是合法的整数格式,会抛出NumberFormatException 闰年判断规则 能被4整除但不能被100整除,或者能被400整除的年份是闰年 逻辑表达式:year%4==0&&year%100!=0||year%400==0 优先级说明:&& 优先级高于 ||,确保判断逻辑正确 六、常见错误与应试技巧 常见错误分析 第一处空白写错包名:如input或output,正确包名是io 第二处空白使用throw而非throws:throw用于抛出具体异常对象,throws用于方法声明 第三处空白用ir调用readLine():InputStreamReader没有readLine()方法,需通过BufferedReader对象in调用 第四处空白直接写字符串:如"s",应传入变量s而非字符串字面量 应试技巧 IO包记忆:输入输出相关类都在java.io包中 输入流链模板:BufferedReader in = new BufferedReader(new InputStreamReader(System.in)); 类型转换口诀:字符串转整数用Integer.parseInt(字符串变量) 闰年规则:记住"四年一闰,百年不闰,四百年再闰"的判断逻辑 通过本题,我们掌握了Java中键盘输入的处理方法、字符串与整数的类型转换,以及闰年判断的逻辑实现。这些知识点在实际开发中常用于数据输入、格式转换和业务逻辑判断,是Java基础编程的重要组成部分,也是计算机二级Java考试的常见考点。