找到
434
篇与
阿贵
相关的结果
- 第 3 页
-
排序算法时间复杂度深度解析：寻找最坏情况下的性能王者 排序算法时间复杂度深度解析：寻找最坏情况下的性能王者 在计算机等级考试二级Java的数据结构部分，排序算法的时间复杂度是必考的重点内容。本文将通过一道典型的选择题，全面解析常见排序算法在最坏情况下的时间复杂度，帮助考生掌握算法性能分析的核心方法。 一、题目回顾 题目内容： 4.png图片 下列排序方法中，最坏情况下时间复杂度最小的是______。 选项： A. 冒泡排序 B. 快速排序 C. 堆排序 D. 希尔排序 二、排序算法时间复杂度总览 在分析最坏情况前，我们先了解各排序算法的平均和最坏时间复杂度： 排序算法平均时间复杂度最坏时间复杂度空间复杂度稳定性冒泡排序O(n²)O(n²)O(1)稳定快速排序O(n log n)O(n²)O(log n)不稳定堆排序O(n log n)O(n log n)O(1)不稳定希尔排序O(n log n)O(n²)O(1)不稳定三、最坏情况深度解析 1. 冒泡排序（选项A） 最坏情况：输入序列完全逆序 时间复杂度：O(n²) 需要进行n-1轮比较 每轮比较n-i次（i为当前轮数） 总比较次数：n(n-1)/2 2. 快速排序（选项B） 最坏情况：每次选择的基准都是当前序列的最大或最小元素 时间复杂度：O(n²) 递归深度达到n层 每层需要进行O(n)次比较 常见场景： 已排序或逆序的输入 所有元素相同 3. 堆排序（选项C） 最坏情况：与输入顺序无关 时间复杂度：O(n log n) 建堆过程：O(n) 每次调整堆：O(log n) 共需调整n-1次 特点： 任何情况下都保持O(n log n) 不受输入数据分布影响 4. 希尔排序（选项D） 最坏情况：取决于增量序列的选择 时间复杂度： 使用希尔增量时：O(n²) 使用Hibbard增量时：O(n^(3/2)) 不确定性： 性能严重依赖增量序列的选择 没有公认的最优增量序列 四、选项对比与正确答案 对比各算法的最坏时间复杂度： 冒泡排序：O(n²) 快速排序：O(n²) 堆排序：O(n log n) 希尔排序：O(n²)（按最保守估计） 显然，堆排序在最坏情况下保持O(n log n)的性能，是四个选项中最好的，因此正确答案是C。 五、常见误区警示 混淆平均情况和最坏情况： 快速排序平均性能很好，但最坏情况很差 不能因为快速排序通常快就选择它 忽略算法稳定性： 虽然本题不考察稳定性，但要注意堆排序和快速排序是不稳定的 希尔排序的增量序列误区： 认为希尔排序总是优于O(n²)，实际上取决于增量选择 堆排序的误解： 认为建堆的O(n)时间复杂度是整个算法的复杂度 六、相关知识扩展 1. 其他排序算法的最坏情况 排序算法最坏时间复杂度插入排序O(n²)选择排序O(n²)归并排序O(n log n)计数排序O(n+k)基数排序O(d(n+k))桶排序O(n²)2. Java中的排序实现 Java的Arrays.sort()方法根据数据类型选择不同算法： 基本类型：快速排序变体（Dual-Pivot QuickSort） 对象类型：归并排序变体（TimSort） int[] arr = {5, 2, 9, 1, 5}; Arrays.sort(arr); // 最坏O(n log n) List<Integer> list = Arrays.asList(5, 2, 9, 1, 5); Collections.sort(list); // 最坏O(n log n)七、解题技巧总结 记忆法： 记住堆排序和归并排序的最坏O(n log n) 记住快速排序的最坏O(n²) 排除法： 先排除明显较差的选项 在剩余选项中比较 特性分析法： 分析各算法的特性决定其最坏情况 实际应用考量： 虽然堆排序最坏情况好，但实际应用中常数因子较大 快速排序通常更快，除非必须保证最坏情况性能 八、模拟练习题 题目1：以下排序算法中，平均和最坏时间复杂度均为O(n log n)的是？ A. 快速排序 B. 插入排序 C. 归并排序 D. 希尔排序 答案分析： 快速排序最坏O(n²) 插入排序最坏O(n²) 归并排序始终O(n log n) 希尔排序最坏O(n²) 正确答案是C。 题目2：对大量数据排序且要求最坏情况下性能稳定，应选用？ A. 冒泡排序 B. 快速排序 C. 堆排序 D. 希尔排序 正确答案是C。 九、备考建议 对比学习：制作对比表格记忆各算法特性 代码实现：亲手实现各排序算法加深理解 性能测试：对不同规模数据测试各算法实际性能 关注应用：了解Java标准库中的排序实现 十、总结 通过这道题目，我们深入理解了： 各排序算法在最坏情况下的性能表现 堆排序在最坏情况下仍保持O(n log n)的优势 快速排序在特定情况下性能会退化 算法选择需要权衡平均性能和最坏情况 关键结论： 堆排序是本题四个选项中最坏情况下时间复杂度最小的排序算法 实际应用中，算法选择需考虑数据特征、规模和要求 Java标准库根据数据类型智能选择排序算法 掌握这些知识不仅有助于应对考试，也为实际编程中的算法选择提供了理论依据。
-
深入解析线性结构的判定：从集合关系到数据结构选择 深入解析线性结构的判定：从集合关系到数据结构选择 在计算机等级考试二级Java的数据结构部分，理解线性结构的本质及其数学表示是重要考点。本文将通过一道典型的选择题，系统讲解如何通过关系R判断数据结构类型，帮助考生掌握线性结构的核心特征和判定方法。 一、题目回顾 题目内容： 3.png图片 设数据元素的集合D={1,2,3,4,5}，则满足下列关系R的数据结构中为线性结构的是______。 选项： A. R={(1,2),(3,2),(5,1),(4,5)} B. R={(1,3),(4,1),(3,2),(5,4)} C. R={(1,2),(2,4),(4,5),(2,3)} D. R={(1,3),(2,4),(3,5),(1,2)} 二、核心概念解析 1. 什么是线性结构？ 线性结构是指数据元素之间存在一对一的关系，具有以下特征： 唯一首元素：没有前驱的元素 唯一尾元素：没有后继的元素 中间元素：有且仅有一个前驱和一个后继 顺序性：元素按序排列，形成线性序列 常见线性结构：数组、链表、栈、队列等 2. 关系R的含义 题目中的关系R表示数据元素之间的前驱-后继关系。例如： (a,b)∈R 表示a是b的前驱，b是a的后继 通过R可以构建出完整的元素排列顺序 三、题目深度解析 判定线性结构的步骤： 检查首元素：找出没有前驱的元素（入度为0） 检查尾元素：找出没有后继的元素（出度为0） 检查中间元素：每个中间元素应有且仅有一个前驱和一个后继 验证连通性：所有元素应能连成一条线，无分叉 对各选项的分析： 选项A：R={(1,2),(3,2),(5,1),(4,5)} 图示关系： 3 → 2 4 → 5 → 1 → 2 问题：元素2有两个前驱（1和3），不符合线性结构要求 结论：非线性 选项B：R={(1,3),(4,1),(3,2),(5,4)} 图示关系： 5 → 4 → 1 → 3 → 2 特点： 首元素：5（无前驱） 尾元素：2（无后继） 每个中间元素只有一个前驱和一个后继 结论：线性结构（顺序：5→4→1→3→2） 选项C：R={(1,2),(2,4),(4,5),(2,3)} 图示关系： 1 → 2 → 4 → 5 ↘ 3 问题：元素2有两个后继（3和4），产生分叉 结论：非线性 选项D：R={(1,3),(2,4),(3,5),(1,2)} 图示关系： 1 → 3 → 5 ↓ 2 → 4 问题：元素1有两个后继（2和3），形成分叉 结论：非线性 四、常见错误分析 忽略唯一性要求： 认为只要元素能连成线就是线性结构（实际上必须严格一对一） 方向混淆： 将前驱和后继关系弄反（注意(a,b)表示a→b） 连通性检查不足： 没有发现存在孤立元素或未连接的元素 多路径误判： 忽略了一个元素有多个前驱或后继的情况 五、相关知识扩展 1. 其他数据结构类型的特征 树形结构： 有且仅有一个根节点 除根外每个节点有且仅有一个前驱 节点可以有多个后继 图状结构： 节点可以有任意数量的前驱和后继 包含环路也是可能的 集合结构： 元素之间没有特定的关系 2. 线性结构的Java实现 在Java中常见的线性结构实现： // 1. 数组（固定大小线性表） int[] array = new int[10]; // 2. ArrayList（动态数组） List<Integer> arrayList = new ArrayList<>(); // 3. LinkedList（链式实现） List<Integer> linkedList = new LinkedList<>(); // 4. Stack（栈，继承自Vector） Stack<Integer> stack = new Stack<>(); // 5. Queue（队列接口） Queue<Integer> queue = new LinkedList<>();六、解题技巧总结 图示法： 将关系R绘制成有向图 观察图形是否符合线性特征 度分析法： 计算每个元素的入度（前驱数量）和出度（后继数量） 线性结构应满足： 首元素：入度=0，出度=1 尾元素：入度=1，出度=0 中间元素：入度=1，出度=1 排除法： 先排除明显不符合的选项（如存在元素有多个前驱/后继） 验证法： 对可能的选项构建完整序列，验证连通性和唯一性 七、模拟练习题 题目：设D={a,b,c,d,e}，以下哪个关系R对应的数据结构是线性结构？ A. R={(a,b),(b,c),(d,e)} B. R={(a,b),(a,c),(b,d)} C. R={(a,b),(b,c),(c,d),(d,e)} D. R={(a,b),(c,b),(d,c)} 答案分析： A：不连通（a→b→c和d→e两部分） B：a有两个后继（分叉） C：完美线性（a→b→c→d→e） D：b有两个前驱 正确答案是C。 八、备考建议 掌握本质：理解线性结构的严格定义，不满足任一条件就不是线性结构 多画图：将抽象的关系转化为直观的图形表示 比较学习：对比线性、树形和图状结构的区别 代码实践：用Java实现各种数据结构，加深理解 九、总结 通过这道题目，我们深入理解了： 线性结构的严格定义和特征 如何通过关系R判断数据结构类型 使用图示法和度分析法解题的技巧 线性结构与其他数据结构的区别 关键记忆点： 线性结构要求严格的一对一关系 首尾元素具有特殊性 中间元素必须恰好一个前驱一个后继 Java集合框架提供了多种线性结构的实现 掌握这些知识不仅有助于应对考试，也为后续学习更复杂的数据结构和算法打下坚实基础。
-
深入解析栈的操作与元素计数：一道计算机二级Java考试的经典题目 深入解析栈的操作与元素计数：一道计算机二级Java考试的经典题目 2.png图片 在准备全国计算机等级考试二级Java的过程中，数据结构部分的栈(Stack)是必考的重点内容。本文将通过一道典型的栈操作题目，详细讲解栈的基本概念、操作原理以及元素计数方法，帮助考生彻底掌握这一重要考点。 一、题目回顾 题目内容如下： 设栈的存储空间为S(1:50)，初始状态为top=51。现经过一系列正常的入栈与退栈操作后，top=50，则栈中的元素个数为______。 选项： A. 50 B. 0 C. 1 D. 49 二、栈的基本概念解析 1. 什么是栈？ 栈(Stack)是一种先进后出(FILO, First In Last Out)的线性数据结构，只允许在一端（称为栈顶）进行插入和删除操作。栈有两个基本操作： 入栈(Push)：将元素放入栈顶 出栈(Pop)：从栈顶取出元素 2. 栈的存储实现 栈通常可以通过数组或链表来实现。本题中使用的是数组实现： 存储空间：S(1:50)表示数组下标从1到50 栈顶指针：top用于指示栈顶位置 三、题目深度解析 1. 初始状态分析 题目给出的初始状态： 存储空间：S(1:50) → 共有50个存储单元 初始top=51 关键理解： 当top=51时，表示栈初始为空（因为存储空间只到50） 这是一种常见的空栈表示方法（top指向存储空间外的第一个位置） 2. 栈操作后的状态 经过一系列入栈和出栈操作后： 最终top=50 3. 元素个数计算 栈中元素个数的计算公式： 元素个数 = 初始top - 当前top计算过程： 初始top=51 当前top=50 元素个数=51-50=1 验证过程： 初始空栈：top=51 第一次入栈：top减1变为50，元素存入S(50) 此时栈中只有一个元素在S(50)，top=50 四、常见错误分析 在解答这类题目时，考生常犯以下错误： 方向混淆： 错误认为top增加表示入栈（实际上在数组实现中，入栈操作通常使top减小） 初始值误解： 认为top=0表示空栈（本题中是top=51表示空栈） 计数公式错误： 使用"当前top-初始top"（应该反过来） 忘记考虑初始状态 边界情况忽略： 没有考虑top超出数组范围的特殊情况 五、相关知识扩展 1. 栈的不同实现方式 数组实现： 固定大小 需要预先分配空间 本题采用的方式 链表实现： 动态大小 不需要预先分配空间 每个节点存储数据和指向下一节点的指针 2. 栈的应用场景 函数调用： 保存函数返回地址 存储局部变量 表达式求值： 中缀表达式转后缀表达式 后缀表达式求值 括号匹配： 检查代码中的括号是否成对出现 浏览器前进后退： 使用两个栈实现页面导航 六、解题技巧总结 画图辅助法： 画出栈的示意图 标记top指针的位置变化 操作模拟法： 模拟入栈和出栈过程 跟踪top值的变化 公式记忆法： 记住元素个数=初始top-当前top 注意初始空栈的top值 边界测试法： 测试极端情况（如空栈、满栈） 七、模拟练习题 为了巩固这一知识点，请尝试解答以下类似题目： 题目：设栈的存储空间为S(1:100)，初始状态为top=101。经过若干次入栈和出栈操作后，top=80，则栈中的元素个数为______。 A. 20 B. 21 C. 80 D. 19 答案分析： 初始top=101，当前top=80 元素个数=101-80=21 正确答案是B。 八、Java中的栈实现 在Java中，可以使用java.util.Stack类或更推荐的Deque接口实现栈： // 使用Stack类 Stack<Integer> stack = new Stack<>(); stack.push(1); // 入栈 int top = stack.pop(); // 出栈 // 使用Deque接口（推荐） Deque<Integer> stack = new ArrayDeque<>(); stack.push(1); int top = stack.pop();九、备考建议 理解原理：不要死记硬背，要理解栈的操作机制 动手实践：自己实现一个栈类，加深理解 多做练习：收集各类栈相关的题目进行练习 注意细节：关注边界条件和特殊情况的处理 十、总结 通过这道题目，我们深入学习了： 栈的基本概念和操作特点 数组实现栈时top指针的变化规律 栈中元素个数的计算方法 常见的错误类型和避免方法 掌握这些知识不仅有助于通过计算机等级考试，也为后续学习更复杂的数据结构打下坚实基础。记住，在数组实现的栈中： 入栈操作使top减小 出栈操作使top增大 元素个数=初始top-当前top 希望本文能帮助你在考试中游刃有余地解答此类题目！
-
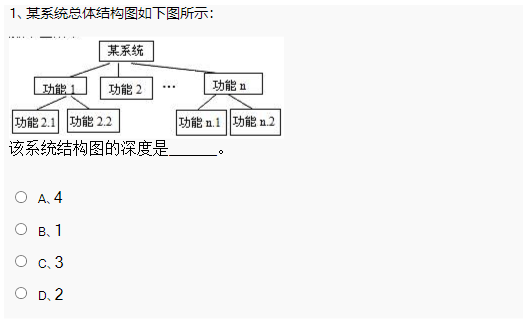
深度解析计算机等级考试二级Java中的"系统结构图深度"问题 深度解析计算机等级考试二级Java中的"系统结构图深度"问题 在准备全国计算机等级考试二级Java的过程中，许多考生对"系统结构图深度"这类题目感到困惑。本文将通过一道典型例题，详细解析系统结构图深度的概念、计算方法及在考试中的应用技巧。 一、题目回顾 题目内容如下： 某系统总体结构图如下图所示： 1.png图片 该系统结构图的深度是______。 选项： A. 4 B. 1 C. 3 D. 2 二、核心概念解析 1. 什么是系统结构图？ 系统结构图（也称为模块结构图）是软件工程中用于表示系统模块组成及调用关系的图形工具。它展示了： 系统的功能模块划分 模块之间的层次关系 模块的调用关系 2. 结构图深度的定义 结构图的深度是指从顶层模块到最底层模块的最长路径上的模块层数。这是软件工程中衡量系统层次复杂度的重要指标之一。 关键点： 从根节点（顶层模块）开始计算 沿着最长路径计算层数 根节点本身记为第1层 三、题目详细解析 让我们分解题目中的结构图： 第1层：某系统（根节点） 第2层：功能1、功能2、功能n 第3层：功能2.1、功能2.2、功能n.1、功能n.2路径分析： 某系统 → 功能1：深度2 某系统 → 功能2 → 功能2.1：深度3 某系统 → 功能2 → 功能2.2：深度3 某系统 → 功能n → 功能n.1：深度3 某系统 → 功能n → 功能n.2：深度3 最长的路径深度为3，因此正确答案是C。 四、常见误区警示 在解答这类题目时，考生常犯以下错误： 混淆深度与宽度： 深度：纵向的层级数 宽度：同一层级中模块的最大数量（本题中第2层宽度为3，第3层宽度为4） 计数方法错误： 错误方法1：从0开始计数（应为从1开始） 错误方法2：只计算叶节点（应计算完整路径） 忽略最长路径： 不是所有路径的深度都相同，需要找出最长的 五、相关考点扩展 在计算机等级考试二级Java的公共基础知识部分，与系统结构图相关的考点还包括： 扇入与扇出： 扇入：调用一个模块的上级模块数量 扇出：一个模块直接调用的下级模块数量 模块独立性： 耦合性：模块间联系的紧密程度 内聚性：模块内部各元素结合的紧密程度 软件结构设计原则： 顶层扇出较高 中间层扇出较少 底层高扇入 六、解题技巧总结 图形还原法： 将文字描述转化为树状图 用缩进关系表示层级（如本文中的图示） 路径追踪法： 从根节点出发，追踪所有可能路径 记录每条路径的深度 选择最大值 快速判断法： 观察功能编号中的小数点数量 如"功能n.2"表示第3层（系统.功能n.功能n.2） 七、模拟练习题 为了巩固这一知识点，请尝试解答以下类似题目： 题目：某系统结构如下： QQ20250707-225337.png图片 该系统的深度是： A. 3 B. 4 C. 5 D. 2 答案分析： 最长路径：订单处理系统 → 订单发货 → 库存扣减 → 库存预警 共4层，因此正确答案是B。 八、备考建议 理解优于记忆：真正掌握深度和宽度的概念，而非死记硬背 多练习画图：将文字描述转化为图形表示 结合软件工程：将这一知识点与模块设计原则联系起来 错题整理：收集同类题目，分析错误原因 九、总结 系统结构图深度是计算机等级考试二级Java公共基础知识部分的重要考点。通过本文的解析，我们了解到： 深度是指从根节点到最远叶节点的层级数 计算时要考虑所有可能路径中的最大值 正确的图形表示有助于快速判断 这一知识点与软件工程中的模块设计密切相关 希望本文能帮助考生在考试中准确解答此类题目，也为后续学习软件工程打下坚实基础。 备考资源：建议参考《软件工程导论》（第6版）中关于软件结构的章节，以及NCRE二级公共基础知识官方教材中的相关内容。
-
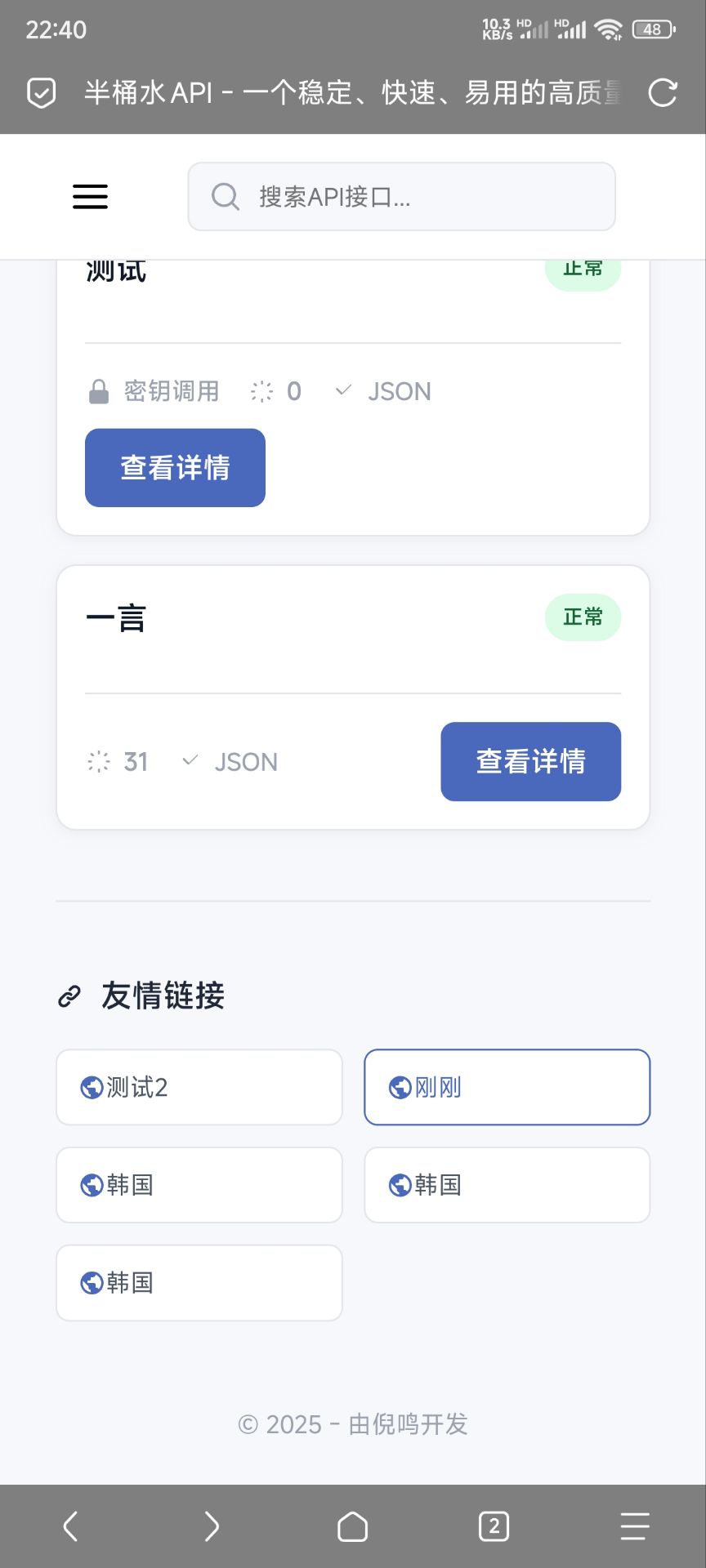
全新升级！导航下载页+API计费系统源码分享：布局优化/友情链接/弹窗公告 全新升级！导航下载页+API计费系统源码分享：布局优化/友情链接/弹窗公告 前言 今天为大家带来全新升级的导航下载页源码，本次更新在原有精美自适应设计基础上，进行了多项实用改进，并额外附赠一套完整的API计费系统源码！这套系统不仅保留了原有的强大功能，还新增了友情链接模块和弹窗式公告系统，使网站更加专业实用。 更新亮点 导航下载页升级内容 首页布局优化：重新设计了首页UI，提升用户体验 友情链接功能：新增友情链接模块，便于网站互推 公告系统升级：将静态公告改为弹窗形式，重要信息更醒目 新增API计费系统 完整的API调用计费解决方案 支持多种计费模式（按次/按时长/按流量） 完善的用户管理和余额系统 API调用统计与分析功能 系统特色 现代化设计语言：采用最新前端技术，视觉效果出众 完全响应式布局：完美适配各种终端设备 双重后台管理：导航站和API系统均有独立后台 智能访问统计：详细记录用户访问行为 多级分类体系：内容组织清晰有序 商业级API系统：可直接用于商业化运营 测试环境 MySQL 5.7+ PHP 8.0+ Redis（可选，用于API缓存） 功能截图 3.jpg图片 搭建教程 导航下载页搭建 解压源码到网站目录 配置.env文件中的数据库信息 导入SQL文件（位置：/database/nav.sql） 设置目录权限（确保storage目录可写） 访问/admin进入后台 API计费系统搭建 解压到独立目录（建议与导航站分开） 配置.env文件 导入SQL文件（位置：/database/api.sql） 配置crontab定时任务（处理过期API密钥等） 访问/admin进入管理后台 常见问题： 确保PHP已安装必要的扩展（mbstring, pdo_mysql等） 伪静态规则需配置正确（Apache/Nginx配置见文档） 首次访问会自动跳转到安装页面（如未跳转请检查重定向规则） 源码下载 导航下载页+API计费系统： 隐藏内容，请前往内页查看详情 代码安全与知识产权保护 推荐使用专业PHP加密服务保护您的商业代码： 推荐加密平台：php.javait.cn 支持的加密方案： 标准加密：SG14～16系列 高级混淆：IC11-12系列 免扩展加密：DECK V1～3 永久免费方案： IC11基础版 DECKV1标准版 最新混淆技术（goto/enphp/noname） 结语 本次分享的升级版导航下载页配合API计费系统，可快速搭建专业级的导航门户和API服务平台。相比市面上动辄上万的商业系统，这套完全开源的解决方案无疑是小成本创业的最佳选择。系统已去除所有内置内容，干净清爽，二次开发方便。 使用提示： 建议先本地测试再上线运营 商业使用时请做好数据备份 可根据需要自行修改UI风格 API系统支持对接支付接口（需自行开发） 如有任何技术问题，欢迎在评论区留言交流！如果觉得资源有用，别忘了点赞收藏哦~
